题目内容
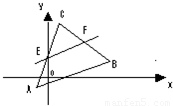
 已知三角形ABC的顶点是A(-1,-1),B(3,1),C(1,6).直线L平行于AB,且分别交AC,BC于E,F,三角形CEF的面积是三角形CAB面积的
已知三角形ABC的顶点是A(-1,-1),B(3,1),C(1,6).直线L平行于AB,且分别交AC,BC于E,F,三角形CEF的面积是三角形CAB面积的| 1 | 4 |
分析:利用三角形CEF的面积是三角形CAB面积的
,得E是CA的中点,由EF∥AB,得直线EF的斜率,从而可求方程
| 1 |
| 4 |
解答:解:由已知,直线AB的斜率K=
,
∵EF∥AB∴直线EF的斜率为 K=
∵三角形CEF的面积是三角形CAB面积的
,∴E是CA的中点.
又点E的坐标(0,
),直线EF的方程是y-
=
x,即x-2y+5=0
| 1 |
| 2 |
∵EF∥AB∴直线EF的斜率为 K=
| 1 |
| 2 |
∵三角形CEF的面积是三角形CAB面积的
| 1 |
| 4 |
又点E的坐标(0,
| 5 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
点评:本题是一个已知三角形的面积求直线方程题目,条件给出的是点的坐标,利用代数方法来解决几何问题,这是解析几何的特点,这是一个典型的数形结合问题

练习册系列答案
相关题目
 .求直线L的方程.
.求直线L的方程.