题目内容
在平面直角坐标系中,若O为坐标原点,则A、B、C三点在同一直线上的充要条件为存在惟一的实数λ,使得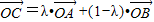 成立,此时称实数λ为“向量
成立,此时称实数λ为“向量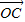 关于
关于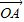 和
和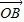 的终点共线分解系数”.若已知P1(3,1)、P2(-1,3),且向量
的终点共线分解系数”.若已知P1(3,1)、P2(-1,3),且向量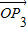 是直线l:x-y+10=0的法向量,则“向量
是直线l:x-y+10=0的法向量,则“向量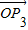 关于
关于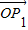 和
和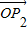 的终点共线分解系数”为 .
的终点共线分解系数”为 .
【答案】分析:由向量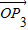 是直线l:x-y+10=0的法向量得出向量
是直线l:x-y+10=0的法向量得出向量 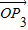 与向量
与向量 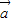 =(1,1)垂直,则由两向量垂直数量积为零,我们可设出向量
=(1,1)垂直,则由两向量垂直数量积为零,我们可设出向量 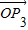 的坐标,然后根据
的坐标,然后根据 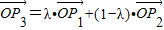 ,我们可以构造一个关于λ的方程组,利用待定系数法即可求出λ的值.
,我们可以构造一个关于λ的方程组,利用待定系数法即可求出λ的值.
解答:解:由向量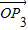 是直线l:x-y+10=0的法向量得出:
是直线l:x-y+10=0的法向量得出: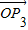 与向量
与向量 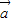 =(1,1)垂直,
=(1,1)垂直,
可设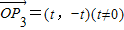 ,
,
由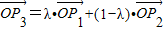
得(t,-t)=λ(3,1)+(1-λ)(-1,3)
=(4λ-1,3-2λ),
∴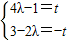 ,
,
两式相加得2λ+2=0,
∴λ=-1.
故答案为:-1.
点评:本小题主要考查向量在几何中的应用、向量共线的充要条件等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.
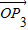 是直线l:x-y+10=0的法向量得出向量
是直线l:x-y+10=0的法向量得出向量 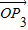 与向量
与向量 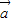 =(1,1)垂直,则由两向量垂直数量积为零,我们可设出向量
=(1,1)垂直,则由两向量垂直数量积为零,我们可设出向量 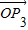 的坐标,然后根据
的坐标,然后根据 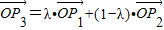 ,我们可以构造一个关于λ的方程组,利用待定系数法即可求出λ的值.
,我们可以构造一个关于λ的方程组,利用待定系数法即可求出λ的值.解答:解:由向量
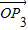 是直线l:x-y+10=0的法向量得出:
是直线l:x-y+10=0的法向量得出: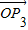 与向量
与向量 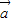 =(1,1)垂直,
=(1,1)垂直,可设
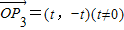 ,
,由
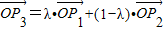
得(t,-t)=λ(3,1)+(1-λ)(-1,3)
=(4λ-1,3-2λ),
∴
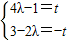 ,
,两式相加得2λ+2=0,
∴λ=-1.
故答案为:-1.
点评:本小题主要考查向量在几何中的应用、向量共线的充要条件等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目