Question

【题目】已知直线的方程为，抛物线：的焦点为，点是抛物线上到直线距离最小的点.

（1）求点的坐标；

（2）若直线与抛物线交于两点，为中点，且，求直线的方程.

Answer 1

【答案】（1）(1,2) （2）9x+3y-7=0

【解析】

(1)根据点到直线的距离公式和二次函数的性质得出P点坐标；(2)设出点M的坐标，由向量坐标化得到M(1,-)，设出点A和点B的坐标，代入抛物线，两式做差得到斜率，由点斜式得到直线方程.

(1)设点P的坐标为(x0,y0),则y02=4x0，所以，点P到直线的距离：

d ====≥

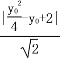当且仅当y0=2时取最小值，此时P点坐标为(1,2).

(2)设点M的坐标为（x1,y1）因为=3, 又点P(1,2),又F(1,0)可得：(0，-2)=3(x1-1,y1-0)

经计算得：点M(1,-)

设点A(x2,y2)点B（x3,y3）,于是

两式相减可得：(y3- y2)( y3+y2)=4(x3-x2) 化简得： =,

所以k=-3

于是，y+=-3(x-1),整理得9x+3y-7=0