题目内容
求证：函数y＝x2－4x＋3有两个不同的零点．
答案：
解析：
解析：
|
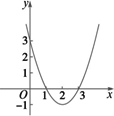
证明：[方法1]考察二次方程2x2＋3x－7＝0．因为Δ＝(－4)2－4×1×3＝16－12＝4＞0， 所以方程x2－4x＋3＝0有两个不相等的实根．因此，二次函数y＝2x2＋3x－7有两个不同的零点． [方法2]设f(x)＝x2－4x＋3，如图，函数的图象是一个开口向上的抛物线，且f(2)＝22－2×4＋3＝－1＜0，
所以函数的图象必与x轴有两个不同的交点，即函数y＝x2－4x＋3有两个不同的零点． [方法3]由二次函数的性质，知 函数在(0，2)上是减函数，在(2，4)上是增函数，且 f(0)＝3＞0，f(2)＝－1＜0，f(4)＝3＞0， 所以函数的图象必与x轴有两个不同的交点， 即函数y＝x2－4x＋3有两个不同的零点． 思路分析：一可利用判断法来证明；二可利用二次函数的图象与x轴交点情况证明． |
练习册系列答案
超能学典应用题题卡系列答案
相关题目
D，同时满足：
不存在“和谐区间”．
(a∈R，a≠0)有“和谐区间”[m，n]，当a变化时，求出n－m的最大值．
}是等差数列；
，求证：Tn＜