题目内容
一个等腰直角三角形的三个顶点分别在正三棱柱的三条侧棱上.已知正三棱柱的底面边长为2,求该三角形的斜边长.分析:如图,设DF长为x,则DE=EF=
x,作DG⊥BB1,HG⊥CC1,EI⊥CC1,从而用x表示出EG,FI,,FH,从而将问题转化到Rt△DHF中,有DF2=DH2+FH2求解.
| ||
| 2 |
解答: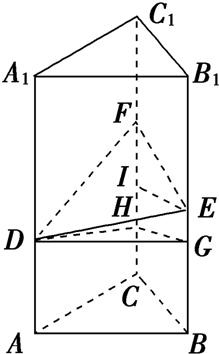 解:如图,正三棱柱ABC-A1B1C1中,△ABC为正三角形,边长为2,△DEF为等腰直角三角形,DF为斜边,设DF长为x,则DE=EF=
解:如图,正三棱柱ABC-A1B1C1中,△ABC为正三角形,边长为2,△DEF为等腰直角三角形,DF为斜边,设DF长为x,则DE=EF=
x,作DG⊥BB1,HG⊥CC1,EI⊥CC1,
则EG=
=
,FI=
=
,FH=FI+HI=FI+EG=2
,在Rt△DHF中,DF2=DH2+FH2,即x2=4+(2
)2,解得x=2
.
即该三角形的斜边长为2
.
 解:如图,正三棱柱ABC-A1B1C1中,△ABC为正三角形,边长为2,△DEF为等腰直角三角形,DF为斜边,设DF长为x,则DE=EF=
解:如图,正三棱柱ABC-A1B1C1中,△ABC为正三角形,边长为2,△DEF为等腰直角三角形,DF为斜边,设DF长为x,则DE=EF=
| ||
| 2 |
则EG=
| DE2-DG2 |
|
| EF2-EI2 |
|
|
|
| 3 |
即该三角形的斜边长为2
| 3 |
点评:本题主要考查棱柱的结构特征,主要涉及了正棱柱,一是底面是正多边形,二是侧棱与底面垂直,还考查了转化思想,属中档题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
 如图,一个等腰直角三角形的硬纸片△ABC中,∠ACB=90°,AC=4cm,CD是斜边上的高,沿CD把△ABC折成直二面角.
如图,一个等腰直角三角形的硬纸片△ABC中,∠ACB=90°,AC=4cm,CD是斜边上的高,沿CD把△ABC折成直二面角. (2013•广州二模)如图,一个等腰直角三角形的直角边长为2,分别以三个顶点为 圆心,l为半径在三角形内作圆弧,三段圆弧与斜边围成区域M (图中白色部分).若在此三角形内随机取一点P,则点P落在区 域M内的概率为
(2013•广州二模)如图,一个等腰直角三角形的直角边长为2,分别以三个顶点为 圆心,l为半径在三角形内作圆弧,三段圆弧与斜边围成区域M (图中白色部分).若在此三角形内随机取一点P,则点P落在区 域M内的概率为