题目内容
已知数列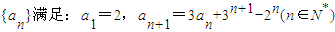 .
.(I)设
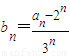 ,证明:数列{bn}为等差数列,并求数列{an}的通项公式;
,证明:数列{bn}为等差数列,并求数列{an}的通项公式;(II)求数列{an}的前n项和Sn;
(III)设
 对一切正整数n均成立,并说明理由.
对一切正整数n均成立,并说明理由.
【答案】分析:(Ⅰ)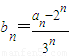 ,利用等差数列的定义,即可证明{bn}为等差数列,公差为1,由此可求数列{an}的通项公式;
,利用等差数列的定义,即可证明{bn}为等差数列,公差为1,由此可求数列{an}的通项公式;
(Ⅱ)利用错位相减法及等比数列的求和公式,即可求得结论;
(Ⅲ)根据通项计算前几项,猜测C1最大,再进行证明.
解答:(Ⅰ)证明:∵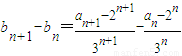 =
=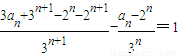 ,
,
∴{bn}为等差数列,公差为1.
又b1=0,∴bn=n-1,∴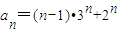 . …(4分)
. …(4分)
(Ⅱ)解:设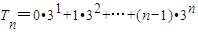 ,则
,则
3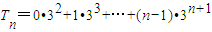 .∴
.∴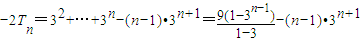 .
.
∴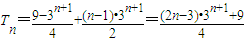 .
.
∴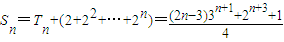 .…(8分)
.…(8分)
(Ⅲ)解:由已知得 ,从而求得
,从而求得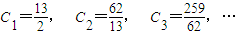
猜测C1最大,下证:
∵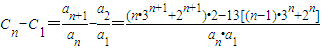 =
=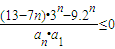 ,
,
∴存在k=1,使得Cn≤Ck对一切正整数n均成立. …(12分)
点评:本题考查等差数列的定义,考查错位相减法求和,考查恒成立问题,正确运用求和是关键.
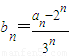 ,利用等差数列的定义,即可证明{bn}为等差数列,公差为1,由此可求数列{an}的通项公式;
,利用等差数列的定义,即可证明{bn}为等差数列,公差为1,由此可求数列{an}的通项公式;(Ⅱ)利用错位相减法及等比数列的求和公式,即可求得结论;
(Ⅲ)根据通项计算前几项,猜测C1最大,再进行证明.
解答:(Ⅰ)证明:∵
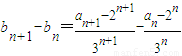 =
=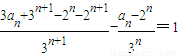 ,
,∴{bn}为等差数列,公差为1.
又b1=0,∴bn=n-1,∴
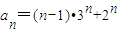 . …(4分)
. …(4分)(Ⅱ)解:设
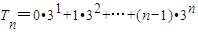 ,则
,则3
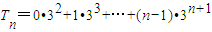 .∴
.∴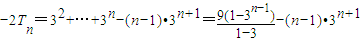 .
.∴
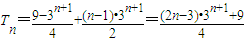 .
.∴
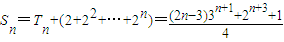 .…(8分)
.…(8分)(Ⅲ)解:由已知得
 ,从而求得
,从而求得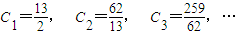
猜测C1最大,下证:
∵
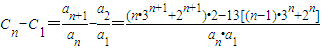 =
=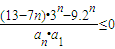 ,
,∴存在k=1,使得Cn≤Ck对一切正整数n均成立. …(12分)
点评:本题考查等差数列的定义,考查错位相减法求和,考查恒成立问题,正确运用求和是关键.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
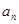 }中
}中
 ,求证数列{
,求证数列{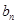 }是等比数列;
}是等比数列; .
.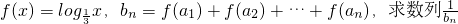 的前n项和Tn.
的前n项和Tn.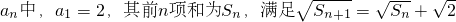 .
.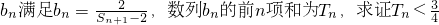 .
.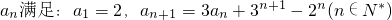 .
.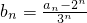 ,证明:数列{bn}为等差数列,并求数列{an}的通项公式;
,证明:数列{bn}为等差数列,并求数列{an}的通项公式;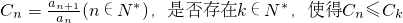 对一切正整数n均成立,并说明理由.
对一切正整数n均成立,并说明理由.