题目内容
已知数列 .
.
(I)求数列{an}的通项公式;
(II)设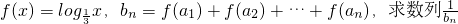 的前n项和Tn.
的前n项和Tn.
解:(I)由S1=a1= (1-a1),得a1=
(1-a1),得a1= ;
;
当n≥2时,an= (1-an)-
(1-an)- (1-an-1)=
(1-an-1)= an+
an+ an-1
an-1
∴ =
= ,
,
∴数列{an}是首项为 ,公比为
,公比为 的等比数列,∴an=
的等比数列,∴an= ×
× =
= :
:
(II)∵f(x)=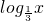 ,
,
∴bn=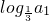 +
+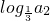 +…+
+…+ =
=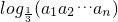 =
=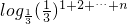 =1+2+3+…+n=
=1+2+3+…+n=
∴ =
=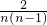 =2(
=2( ),
),
∴Tn=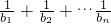 =2[(1-
=2[(1- )+(
)+(
 )+…+(
)+…+( )]=
)]= .
.
分析:(I)根据数列的性质S1=a1可以求出a1的值,然后再利用递推公式相减,从而推出数列{an}为等比数列,从而求解;
(II)由(I)知an的通项公式把a1到an代入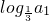 +
+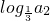 +…+
+…+ ,然后再求其倒数,可以发现
,然后再求其倒数,可以发现 =2(
=2( ),从而得其前n项和Tn.
),从而得其前n项和Tn.
点评:此题考查等比数列的性质及其前n项和,第一问比较基础还是应用递推公式相减,第二问要充分利用第一问的结论,这一点以后做题时要注意.
 (1-a1),得a1=
(1-a1),得a1= ;
;当n≥2时,an=
 (1-an)-
(1-an)- (1-an-1)=
(1-an-1)= an+
an+ an-1
an-1∴
 =
= ,
,∴数列{an}是首项为
 ,公比为
,公比为 的等比数列,∴an=
的等比数列,∴an= ×
× =
= :
:(II)∵f(x)=
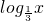 ,
,∴bn=
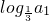 +
+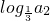 +…+
+…+ =
=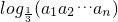 =
=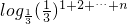 =1+2+3+…+n=
=1+2+3+…+n=
∴
 =
=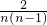 =2(
=2( ),
),∴Tn=
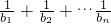 =2[(1-
=2[(1- )+(
)+(
 )+…+(
)+…+( )]=
)]= .
.分析:(I)根据数列的性质S1=a1可以求出a1的值,然后再利用递推公式相减,从而推出数列{an}为等比数列,从而求解;
(II)由(I)知an的通项公式把a1到an代入
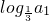 +
+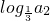 +…+
+…+ ,然后再求其倒数,可以发现
,然后再求其倒数,可以发现 =2(
=2( ),从而得其前n项和Tn.
),从而得其前n项和Tn.点评:此题考查等比数列的性质及其前n项和,第一问比较基础还是应用递推公式相减,第二问要充分利用第一问的结论,这一点以后做题时要注意.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2013•潍坊一模)已知数列{an}的各项排成如图所示的三角形数阵,数阵中每一行的第一个数a1,a2,a4,a7,…构成等差数列{bn},Sn是{bn}的前n项和,且b1=a1=1,S5=15.
(2013•潍坊一模)已知数列{an}的各项排成如图所示的三角形数阵,数阵中每一行的第一个数a1,a2,a4,a7,…构成等差数列{bn},Sn是{bn}的前n项和,且b1=a1=1,S5=15. (2013•潍坊一模)已知数列{an}的各项排成如图所示的三角形数阵,数阵中每一行的第一个数a1,a2,a4,a7,…构成等差数列{bn},Sn是{bn}的前n项和,且b1=a1=1,S5=15.
(2013•潍坊一模)已知数列{an}的各项排成如图所示的三角形数阵,数阵中每一行的第一个数a1,a2,a4,a7,…构成等差数列{bn},Sn是{bn}的前n项和,且b1=a1=1,S5=15.