题目内容
已知定义在R上的函数f(x)满足下面两个条件:
①对于任意的x,y∈R,都有f(x+y)=f(x)+f(y)
②当x>0时,f(x)<0
(1)判断f(x)的奇偶性,并证明;
(2)判断f(x)的单调性,并证明;
(3)如果不等式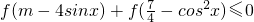 对于任意x∈R都成立,求实数m的取值范围.
对于任意x∈R都成立,求实数m的取值范围.
解:(1)取x=y=0,可得f(0)=0,
再取y=-x,可得f(x)+f(-x)=f(0)=0,
所以f(-x)=-f(x),f(x)是奇函数 …(5分)
(2)任取x1<x2,则 f(x2)-f(x1)=f(x2)+f(-x1)=f(x2-x1)<0,
可得 f(x1)>f(x2),所以f(x) 在R上是减函数 …(10分)
(3)∵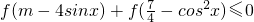 ,且f(x)是奇函数
,且f(x)是奇函数
∴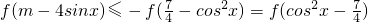
∵f(x) 在R上是减函数
∴ ,即
,即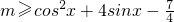
∴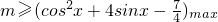
∴下面即求函数 的最大值
的最大值
由于 =
=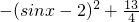 ,sinx∈[-1,1]
,sinx∈[-1,1]
∴当且仅当sinx=1时,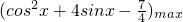 =
=
所以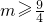 …(16分)
…(16分)
分析:(1)根据已知等式,采用赋值法结合函数奇偶性的定义,可得f(x)是奇函数;
(2)根据函数单调性的定义,任取x1<x2,将 f(x2)与f(x1)作差得到负数,从而 f(x1)>f(x2),得到f(x) 在R上是减函数;
(3)根据函数在R上是奇函数且为减函数,将原不等式转化为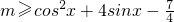 在R上恒成立,再根据二次函数在闭区间上的最值,得到不等式右边的最大值,从而得到实数m的取值范围.
在R上恒成立,再根据二次函数在闭区间上的最值,得到不等式右边的最大值,从而得到实数m的取值范围.
点评:本题着重考查了函数的单调性与奇偶性、复合三角函数的最值和不等式恒成立问题的处理等知识,属于中档题.
再取y=-x,可得f(x)+f(-x)=f(0)=0,
所以f(-x)=-f(x),f(x)是奇函数 …(5分)
(2)任取x1<x2,则 f(x2)-f(x1)=f(x2)+f(-x1)=f(x2-x1)<0,
可得 f(x1)>f(x2),所以f(x) 在R上是减函数 …(10分)
(3)∵
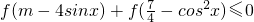 ,且f(x)是奇函数
,且f(x)是奇函数∴
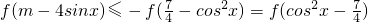
∵f(x) 在R上是减函数
∴
 ,即
,即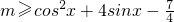
∴
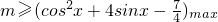
∴下面即求函数
 的最大值
的最大值由于
 =
=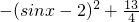 ,sinx∈[-1,1]
,sinx∈[-1,1]∴当且仅当sinx=1时,
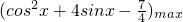 =
=
所以
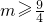 …(16分)
…(16分)分析:(1)根据已知等式,采用赋值法结合函数奇偶性的定义,可得f(x)是奇函数;
(2)根据函数单调性的定义,任取x1<x2,将 f(x2)与f(x1)作差得到负数,从而 f(x1)>f(x2),得到f(x) 在R上是减函数;
(3)根据函数在R上是奇函数且为减函数,将原不等式转化为
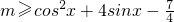 在R上恒成立,再根据二次函数在闭区间上的最值,得到不等式右边的最大值,从而得到实数m的取值范围.
在R上恒成立,再根据二次函数在闭区间上的最值,得到不等式右边的最大值,从而得到实数m的取值范围.点评:本题着重考查了函数的单调性与奇偶性、复合三角函数的最值和不等式恒成立问题的处理等知识,属于中档题.

练习册系列答案
相关题目
已知定义在R上的函数f(x),对任意x∈R,都有f(x+6)=f(x)+f(3)成立,若函数y=f(x+1)的图象关于直线x=-1对称,则f(2013)=( )
| A、0 | B、2013 | C、3 | D、-2013 |