题目内容
2.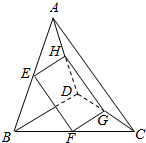 如图,三棱锥A-BCD中,AB=BC=CD=DA=BD=AC=2a,E,F,G,H分别是AB,BC,CD,DA的中点.
如图,三棱锥A-BCD中,AB=BC=CD=DA=BD=AC=2a,E,F,G,H分别是AB,BC,CD,DA的中点.(1)证明四边形EFGH是四边形
(2)求多面体BD-EFGH的体积.
分析 (1)在△ABC中,E、F分别是边AB、BC中点,得到EF∥AC,且EF=$\frac{1}{2}$AC,GH∥AC,且GH=$\frac{1}{2}$AC,得到四边形EFGH是平行四边形.
(2)求出三棱锥的体积,由对称性易知平面EFGH将正四面体两等分,即可得出结论.
解答 (1)证明:在△ABC中,E、F分别是边AB、BC中点,
所以EF∥AC,且EF=$\frac{1}{2}$AC,
同理有GH∥AC,且GH=$\frac{1}{2}$AC,
∴EF∥GH且EF=GH,
故四边形EFGH是平行四边形.
(2)解:显然这个三棱锥是正四面体,高为$\sqrt{(2a)^{2}-(\frac{2\sqrt{3}}{3}a)^{2}}$=$\frac{2\sqrt{6}}{3}$a,其体积为V=$\frac{1}{3}•\frac{\sqrt{3}}{4}•4{a}^{2}•\frac{2\sqrt{6}}{3}a$=$\frac{2\sqrt{2}}{3}{a}^{3}$,
∵AB=BC=CD=DA=BD=AC=2a,E,F,G,H分别是AB,BC,CD,DA的中点,
∴四边形EFGH为正方形.
由对称性易知平面EFGH将正四面体两等分,
∴多面体BD-EFGH的体积为$\frac{\sqrt{2}}{3}{a}^{3}$.
点评 主要考查知识点:简单几何体和公理四,多面体BD-EFGH的体积.公理四:和同一条直线平行的直线平行.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
17.若输出的i=5,则k的最小正整数值为( )
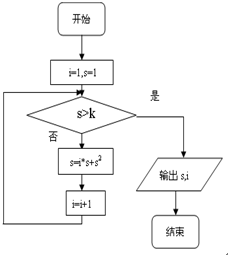

| A. | 88 | B. | 89 | C. | 8095 | D. | 8096 |
7.已知直角三角形ABC,其三边分为a,b,c,(a>b>c).分别以三角形的a边,b边,c边所在直线为轴旋转一周形成三个几何体,其体积分别为V1,V2,V3,则它们的关系为( )
| A. | V1>V2>V3 | B. | V1<V2<V3 | C. | V1=V2<V3 | D. | V1<V2=V3 |
11.已知随机变量X服从正态分布N(3,1),且P(X>4)=0.1587,则P(2≤X≤4)等于( )
| A. | 0.3413 | B. | 0.1585 | C. | 0.8413 | D. | 0.6826 |
12.定义运算“*”如下:x*y=$\left\{\begin{array}{l}{x,x≥y}\\{y,x<y}\end{array}\right.$,若函数f(x)=(1-2x)*(2x-3),则f(x)等于( )
| A. | $\left\{\begin{array}{l}1-{2}^{x},x≤1\\{2}^{x}-3,x>1\end{array}\right.$ | B. | $\left\{\begin{array}{l}{{2}^{x}-3,x<1}\\{1-{2}^{x},x≥1}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{{2}^{x}-4,x≥1}\\{2-{2}^{x},x<1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{{4}^{x}-3,x<1}\\{1-{4}^{x},x≥1}\end{array}\right.$ |