题目内容
抛物线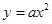 的准线方程为
的准线方程为 ,则实数
,则实数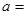 ( )
( )
| A.4 | B.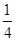 | C.2 | D. |
B
解析试题分析:根据题意,由于抛物线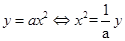 ,g故可知焦点在y轴上,开口向上,因此准线方程为y=-1,那么可知
,g故可知焦点在y轴上,开口向上,因此准线方程为y=-1,那么可知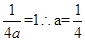 ,故选B.
,故选B.
考点:抛物线的性质
点评:解决的关键是确定焦点位置,以及准线方程的表示,属于基础题。

练习册系列答案
相关题目
F1、F2是定点,|F1F2|=6,动点M满足|MF1|+|MF2|=8,则点M的轨迹是( )
| A.线段 | B.直线 | C.椭圆 | D.圆 |
直线 过点
过点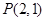 与曲线
与曲线 恰有一个公共点,则满足条件的直线
恰有一个公共点,则满足条件的直线 的条数为( )
的条数为( )
| A.1 | B.2 | C.3 | D.4 |
抛物线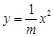 的焦点坐标为( )
的焦点坐标为( )
A.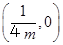 | B.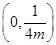 | C.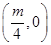 | D.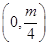 |
若 的焦点与
的焦点与 的左焦点重合,则
的左焦点重合,则 ( )
( )
| A.-2 | B.2 | C.-4 | D.4 |
抛物线y=x2在点M(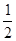 ,
,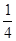 )处的切线的倾斜角是( )
)处的切线的倾斜角是( )
| A.30° | B.45° | C.60° | D.90° |
斜率为 的直线与双曲线
的直线与双曲线 (a>0,b>0)恒有两个公共点,则双曲线离心率的取值范围是
(a>0,b>0)恒有两个公共点,则双曲线离心率的取值范围是
A. | B. | C. | D. |
已知函数 是偶函数,则函数的图象与y轴交点的纵坐标的最大值为:( )
是偶函数,则函数的图象与y轴交点的纵坐标的最大值为:( )
| A.-4 | B.2 | C.3 | D.4 |
 相切倾斜角为
相切倾斜角为 的直线
的直线 与
与 轴和
轴和 轴的交点分别是A和B,那么过A、B两点的最小圆截抛物线
轴的交点分别是A和B,那么过A、B两点的最小圆截抛物线 C.2 D.
C.2 D.