题目内容
已知函数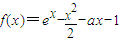 ,(其中a∈R,e为自然对数的底数
,(其中a∈R,e为自然对数的底数(1)当a=0时,求曲线y=f(x)在(0,f(0))处的切线方程;
(2)当x≥1时,若关于x的不等式f(x)≥0恒成立,求实数a的取值范围.
【答案】分析:(1)当a=0时求出f(x)的解析式,根据导数的几何意义求出函数f(x)在x=0处的导数,从而求出切线的斜率,再用点斜式写出切线方程,化成斜截式即可.
(2)将a分离出来得a≤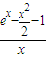 ,设
,设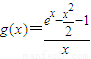 ,然后利用导数研究函数g(x)在[1,+∞)上单调性,求出g(x)的最小值,使a≤g(x)min即可.
,然后利用导数研究函数g(x)在[1,+∞)上单调性,求出g(x)的最小值,使a≤g(x)min即可.
解答:解:(1)当a=0时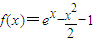 ,∴f'(x)=ex-x,∴f(0)=0,f'(0)=1,∴切线方程为y=x.(4分)
,∴f'(x)=ex-x,∴f(0)=0,f'(0)=1,∴切线方程为y=x.(4分)
(2)∵x≥1,∴ ≥0?a≤
≥0?a≤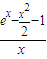 ,(5分)
,(5分)
设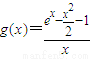 ,则
,则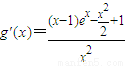 ,(7分)
,(7分)
设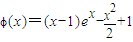 ,则ϕ'(x)=x(ex-1)>0,(9分)
,则ϕ'(x)=x(ex-1)>0,(9分)
∴ϕ(x)在[1,+∞)上为增函数,∴ϕ(x)≥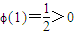 ,∴
,∴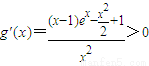 ,
,
∴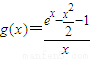 在[1,+∞)上为增函数,∴g(x)≥
在[1,+∞)上为增函数,∴g(x)≥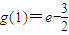 ,∴a≤
,∴a≤ .(12分)
.(12分)
点评:本题主要考查了利用导数研究曲线上某点切线方程,以及函数恒成立问题等有关知识,同时考查了计算能力,属于中档题.
(2)将a分离出来得a≤
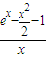 ,设
,设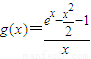 ,然后利用导数研究函数g(x)在[1,+∞)上单调性,求出g(x)的最小值,使a≤g(x)min即可.
,然后利用导数研究函数g(x)在[1,+∞)上单调性,求出g(x)的最小值,使a≤g(x)min即可.解答:解:(1)当a=0时
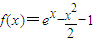 ,∴f'(x)=ex-x,∴f(0)=0,f'(0)=1,∴切线方程为y=x.(4分)
,∴f'(x)=ex-x,∴f(0)=0,f'(0)=1,∴切线方程为y=x.(4分)(2)∵x≥1,∴
 ≥0?a≤
≥0?a≤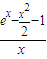 ,(5分)
,(5分)设
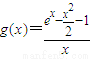 ,则
,则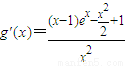 ,(7分)
,(7分)设
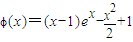 ,则ϕ'(x)=x(ex-1)>0,(9分)
,则ϕ'(x)=x(ex-1)>0,(9分)∴ϕ(x)在[1,+∞)上为增函数,∴ϕ(x)≥
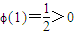 ,∴
,∴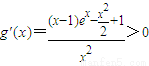 ,
,∴
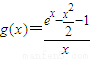 在[1,+∞)上为增函数,∴g(x)≥
在[1,+∞)上为增函数,∴g(x)≥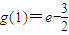 ,∴a≤
,∴a≤ .(12分)
.(12分)点评:本题主要考查了利用导数研究曲线上某点切线方程,以及函数恒成立问题等有关知识,同时考查了计算能力,属于中档题.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
 .,其中a,b∈R
.,其中a,b∈R ,
, (其中A>0,
(其中A>0, >0,
>0, <
<
 的部分图象如图所示,求这个函数的解析式.
的部分图象如图所示,求这个函数的解析式.
 满足
满足 ,其中a>0,a≠1.
,其中a>0,a≠1.
 的值为负数,求
的值为负数,求 的取值范围。
的取值范围。 (其中A>0,
(其中A>0, )的图象如图所示。
)的图象如图所示。
 的值。
的值。