题目内容
已知△BCD中,∠BCD=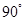 ,BC=CD=1,AB⊥平面BCD,∠ADB=
,BC=CD=1,AB⊥平面BCD,∠ADB=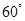 ,E、F分别是AC、AD上的动点,且
,E、F分别是AC、AD上的动点,且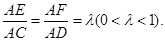
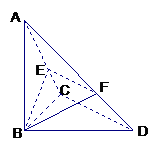
(Ⅰ)求证:不论λ为何值,总有平面BEF⊥平面ABC;
(Ⅱ)当λ为何值时,平面BEF⊥平面ACD ?
(1)对于探索性问题中的的求解,一般是假设存在成立,然后结合已知的结论,逆向推理分析,得到证明。
(2)对于面面垂直的证明,一般先证明线面垂直,然后根据面面垂直的判定定理来加以证明。
解析试题分析:证明:(Ⅰ)∵AB⊥平面BCD, ∴AB⊥CD,
∵CD⊥BC且AB∩BC=B, ∴CD⊥平面ABC.
又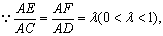 ∴不论λ为何值,恒有EF∥CD,∴EF⊥平面ABC,EF
∴不论λ为何值,恒有EF∥CD,∴EF⊥平面ABC,EF 平面BEF,∴不论λ为何值恒有平面BEF⊥平面ABC.
平面BEF,∴不论λ为何值恒有平面BEF⊥平面ABC.
(Ⅱ)由(Ⅰ)知,BE⊥EF,又平面BEF⊥平面ACD,
∴BE⊥平面ACD,∴BE⊥AC.
∵BC=CD=1,∠BCD=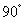 ,∠ADB=
,∠ADB=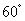 ,
,
∴
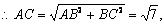 由
由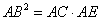 得
得
故当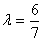 时,平面BEF⊥平面ACD.
时,平面BEF⊥平面ACD.
考点:空间中面面垂直的证明
点评:解决的关键是假设满足题意,然后逆向分析得到垂直的条件 ,进而分析求解,属于基础题。

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
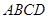 中,
中, ,
, ,且
,且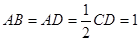 .
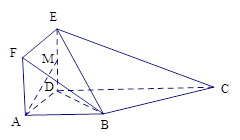
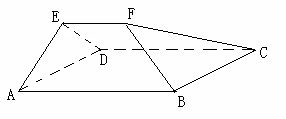
. 为一边向形外作正方形
为一边向形外作正方形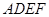 ,然后沿边
,然后沿边 为
为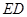 的中点,如图2.
的中点,如图2.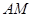 ∥平面
∥平面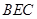 ;
;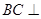 平面
平面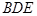 ;
; 到平面
到平面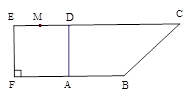
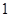 图
图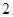
 平面ABCD,EF∥AB, AB=2EF=2AD=4,
平面ABCD,EF∥AB, AB=2EF=2AD=4,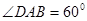 .
.

 中,
中, 底面
底面 ,
,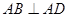 ,
,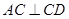 ,
,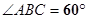 ,
,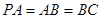 ,
,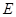 是
是 的中点.
的中点.
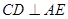 ;
; 平面
平面 ;
; 的余弦值.
的余弦值.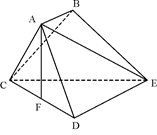
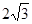 , BC=6.
, BC=6.
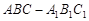 中,
中,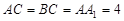 ,
, 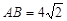 ,若
,若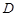 是
是 中点.
中点.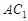 ∥平面
∥平面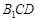 ;
; 所成的角.
所成的角.