题目内容
3. 已知点F是抛物线C1:x2=4y的焦点,过抛物线上一点P,作抛物线的切线l,切点P在第一象限,如图,切线l与椭圆C2:$\frac{{y}^{2}}{4}$+$\frac{{x}^{2}}{3}$=1相交于不同的两点A、B.
已知点F是抛物线C1:x2=4y的焦点,过抛物线上一点P,作抛物线的切线l,切点P在第一象限,如图,切线l与椭圆C2:$\frac{{y}^{2}}{4}$+$\frac{{x}^{2}}{3}$=1相交于不同的两点A、B.(1)若|FA|、|FP|、|FB|依次成等差数列,求直线l的方程;
(2)设定点M(0,$\frac{4}{3}$),求△MAB的面积S的最大值.
分析 (1)利用抛物线与椭圆有公共焦点,且椭圆的离心率为$\frac{1}{2}$,设P(2t,t2),运用导数求得切线的斜率,得到切线方程,联立椭圆方程,运用韦达定理,再由等差数列的性质,结合抛物线和椭圆的定义,计算可得t的方程,解得t,即可得到切线方程;
(2)运用点到直线的距离公式和弦长公式,由三角形的面积公式,化简整理,再由二次函数的最值,即可得到最大值.
解答 解:(1)点F的坐标为(0,1),
椭圆C2:$\frac{{y}^{2}}{4}$+$\frac{{x}^{2}}{3}$=1的a=2,b=$\sqrt{3}$,即有c=1,e=$\frac{1}{2}$,
F(0,1)为椭圆的上焦点,
设P(2t,t2),由y′=$\frac{1}{2}$x,得切线的斜率为t,
从而切线l的方程为y=tx-t2,
直线l与椭圆方程联立,得(3t2+4)x2-6t3x+3t4-12=0,
即有判别式△=36t6-4(3t2+4)(3t4-12)>0,解得t2<4.
设A(x1,y1),B(x2,y2),则x1+x2=$\frac{6{t}^{3}}{3{t}^{2}+4}$,x1x2=$\frac{3{t}^{4}-12}{3{t}^{2}+4}$,
即有y1+y2=t(x1+x2)-2t2=$\frac{6{t}^{4}}{3{t}^{2}+4}$-2t2=-$\frac{8{t}^{2}}{3{t}^{2}+4}$,
由|FA|、|FP|、|FB|依次成等差数列,
则2|FP|=|FA|+|FB|,
由抛物线的定义可得|FP|=t2+1,
由椭圆的定义可得|FA|=$\frac{1}{2}$(4-y1),|FB|=$\frac{1}{2}$(4-y2),
则有4-$\frac{1}{2}$(y1+y2)=2t2+2,
即有2+$\frac{4{t}^{2}}{3{t}^{2}+4}$=2t2,化简得3t4-t2-4=0,
解得t2=$\frac{4}{3}$,即有t=$\frac{2\sqrt{3}}{3}$(负值舍去).
即有直线l:y=$\frac{2\sqrt{3}}{3}$x-$\frac{4}{3}$;
(2)由(1)可得M(0,$\frac{4}{3}$)到切线l的距离为d=$\frac{|\frac{4}{3}+{t}^{2}|}{\sqrt{1+{t}^{2}}}$,
弦长|AB|=$\sqrt{1+{t}^{2}}$•$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{1+{t}^{2}}$•$\sqrt{\frac{36{t}^{6}}{(3{t}^{2}+4)^{2}}-\frac{4(3{t}^{4}-12)}{3{t}^{2}+4}}$
=$\sqrt{1+{t}^{2}}$•$\frac{\sqrt{-48({t}^{4}-3{t}^{2}-4)}}{3{t}^{2}+4}$,(t2<4),
即有△MAB的面积为S=$\frac{1}{2}$d•|AB|=$\frac{2\sqrt{3}}{3}$$\sqrt{-{t}^{4}+3{t}^{2}+4}$=$\frac{2\sqrt{3}}{3}$$\sqrt{-({t}^{2}-\frac{3}{2})^{2}+\frac{25}{4}}$
则当t2=$\frac{3}{2}$时,△MAB的面积取得最大值,且为$\frac{5}{3}\sqrt{3}$.
点评 本题考查抛物线和椭圆的定义、方程和性质,主要考查定义法解题,同时考查直线与椭圆的位置关系,考查韦达定理和弦长公式的运用,借助二次函数的性质解决最值问题,属于中档题.

 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | b>c>a |
| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | 0 |
 如图,直线y=m与抛物线y2=4x交于点A,与圆(x-1)2+y2=4的实线部分交于点B,F为抛物线的焦点,则三角形ABF的周长的取值范围是(4,6).
如图,直线y=m与抛物线y2=4x交于点A,与圆(x-1)2+y2=4的实线部分交于点B,F为抛物线的焦点,则三角形ABF的周长的取值范围是(4,6).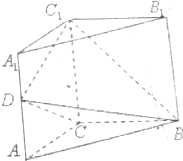 如图,直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=$\frac{1}{2}$AA1,D是棱AA1上的动点.
如图,直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=$\frac{1}{2}$AA1,D是棱AA1上的动点.