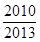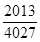题目内容
直线 的方向向量为
的方向向量为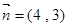 且过抛物线
且过抛物线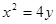 的焦点,则直线
的焦点,则直线 与抛物线围成的封闭图形面积为( )
与抛物线围成的封闭图形面积为( )
A.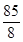 | B.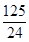 | C.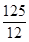 | D.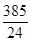 |
B
解析试题分析:由题可得直线l的斜率为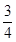 ,抛物线的焦点为
,抛物线的焦点为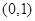 ,所以直线l的方程为
,所以直线l的方程为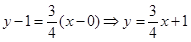 .联立直线与抛物线方程
.联立直线与抛物线方程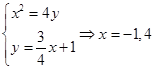 ,则可知直线
,则可知直线 与抛物线围成的封闭图形面积为
与抛物线围成的封闭图形面积为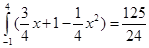 ,故选B.
,故选B.
考点:直线方程 定积分

练习册系列答案
相关题目
由曲线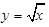 ,直线
,直线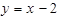 及
及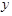 轴所围成的封闭图形的面积为( )
轴所围成的封闭图形的面积为( )
A.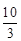 | B.4 | C.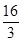 | D.6 |
如果一个物体的运动方程为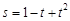 ,其中s的单位是米,t的单位是秒,那么物体在3秒末的瞬时速度是( )
,其中s的单位是米,t的单位是秒,那么物体在3秒末的瞬时速度是( )
| A.7米/秒 | B.6米/秒 | C.5米/秒 | D.8米/秒 |
若函数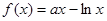 在
在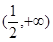 内单调递增,则
内单调递增,则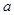 的取值范围为( )
的取值范围为( )
A.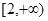 | B.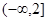 | C.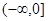 | D.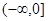 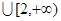 |
对于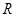 上可导的任意函数
上可导的任意函数 ,若满足
,若满足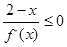 ,则必有( )
,则必有( )
A.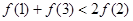 | B.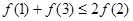 |
C.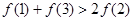 | D.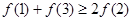 |
定义在R上的函数f(x)满足(x+2)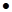 f’(x)<0,又a=f(log0.53),b=f((
f’(x)<0,又a=f(log0.53),b=f((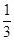 )0.3),c=f(ln3),则( )
)0.3),c=f(ln3),则( )
| A.a<b<c | B.b<c<a | C.c<a<b | D.c< b<a |
函数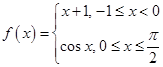 的图象与
的图象与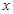 轴所围成的封闭图形的面积为( )
轴所围成的封闭图形的面积为( )
A.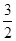 | B.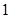 | C. | D. |
函数f(x)=2lnx+x2-bx+a(b>0,a∈R)在点(b,f(b))处的切线斜率的最小值是( )
A.2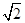 | B.2 | C.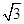 | D.1 |
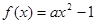 的图像在点A(1,f(1))处的切线l与直线
的图像在点A(1,f(1))处的切线l与直线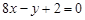 平行,若数列
平行,若数列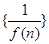 的前
的前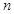 项和为
项和为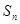 ,则
,则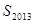 的值为( )
的值为( )