题目内容
【题目】如图所示，某桥是抛物线形拱桥，当水面在l时，拱顶离水面2 m，水面宽4 m．
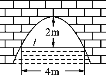
（1）水位下降1 m后，计算水面宽多少米？
（2）已知经过上述抛物线焦点且斜率为2的直线交抛物线于A、B两点，求A、B两点间的距离
．
【答案】（1）
（2）10
【解析】
（1）先建立直角坐标系，设抛物线方程为
,将点（-2，-2）代入抛物线方程求得p，得到抛物线方程，再把y＝﹣3代入抛物线方程求得x0进而得到答案．
（2）先由焦点坐标及斜率为2得到直线方程，联立方程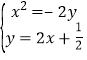
,
得
，有
,代入弦长公式
，即可求解.
（1）以拱顶为坐标原点建立直角坐标系，水平向右为x轴正方向，竖直向上为y轴正方向.设抛物线方程为,
将点（-2，-2）代入解得
=
,
,
代入
得
,
水面宽为m.
（2）抛物线方程为
，焦点（
）,
即直线方程为
,
联立方程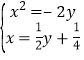
,
得，
有,
焦点在y轴负半轴，由焦点弦公式得
.
练习册系列答案
相关题目
【题目】某种产品的广告费支出
与销售额
(单位：万元）具有较强的相关性，且两者之间有如下对应数据:
| 2 | 4 | 5 | 6 | 8 |
| 28 | 36 | 52 | 56 | 78 |
（1）求关于的线性回归方程
；
（2）根据（1）中的线性回归方程，当广告费支出为10万元时，预测销售额是多少？
参考数据： 
，
，
。
附：回归方程中斜率和截距的最小二乘估计公式分别为：
，
.
