题目内容
【题目】如图,正方形ACDE所在的平面与平面ABC垂直,M是CE和AD的交点,![]() ,且
,且![]()
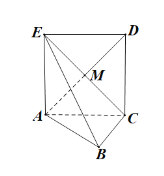
(1)求证:![]() 平面
平面![]() ;
;
(2)求三棱锥![]() 的体积.
的体积.
(3)求二面角![]() 的大小.
的大小.
【答案】(1)证明见解析.(2)![]() .(3)
.(3)![]()
【解析】
以点![]() 为原点,以过
为原点,以过![]() 点平行于
点平行于![]() 的直线为
的直线为![]() 轴,以
轴,以![]() 和
和![]() 为
为![]() 轴和
轴和![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() .
.
(1)根据线面垂直的判定定理,只要证![]() ,
,![]() ,则问题可证;
,则问题可证;
(2)由题意易得![]() 平面
平面![]() ,所以将
,所以将![]() 看成底面,
看成底面,![]() 为高,利用等体积法求解.
为高,利用等体积法求解.
(3)根据题意,求得平面![]() 的一个法向量为
的一个法向量为![]() ,又
,又![]() 为平面
为平面![]() 的一个法向量,代入
的一个法向量,代入![]() 求解.
求解.
![]() 四边形
四边形![]() 是正方形,
是正方形,
![]() ,
,
![]() 平面
平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
![]() 以点
以点![]() 为原点,以过
为原点,以过![]() 点平行于
点平行于![]() 的直线为
的直线为![]() 轴,以
轴,以![]() 和
和![]() 为
为![]() 轴和
轴和![]() 轴,建立如图空间直角坐标系
轴,建立如图空间直角坐标系![]() .
.

设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() 是正方形
是正方形![]() 的对角线的交点,
的对角线的交点,
![]() .
.
(1)![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]()
![]() 平面
平面![]() .
.
(2)![]() .
.
(3)设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则![]() 且
且![]() ,
,
![]() 且
且![]() .
.
![]() , 即
, 即![]()
取![]() ,则
,则![]() ,则
,则![]() .
.
又![]() 为平面
为平面![]() 的一个法向量,且
的一个法向量,且![]() ,
,
![]() ,
,
设二面角![]() 的平面角为
的平面角为![]() ,则
,则![]() ,
,
![]() .
.
![]() 二面角
二面角![]() 等于
等于![]() .
.

练习册系列答案
相关题目
【题目】某医院用光电比色计检查尿汞时,得尿汞含量(毫克/升)与消光系数如下表:
尿汞含量 | 2 | 4 | 6 | 8 | 10 |
消光系数 | 64 | 138 | 205 | 285 | 360 |
(1)作散点图;
(2)如果![]() 与
与![]() 之间具有线性相关关系,求回归线直线方程;
之间具有线性相关关系,求回归线直线方程;
(3)估计尿汞含量为9毫克/升时消光系数.
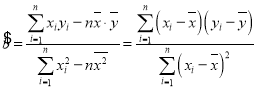 ,
,![]() .
.
参考数据:![]() ,
,![]() .
.