Question

【题目】定义在（0，+∞）上的函数f（x）满足下面三个条件：
①对任意正数a，b，都有f（a）+f（b）=f（ab）；
②当x＞1时，f（x）＜0；
③f（2）=﹣1
（I）求f（1）和 的值；
（II）试用单调性定义证明：函数f（x）在（0，+∞）上是减函数；
（III）求满足f（log4x）＞2的x的取值集合．

Answer 1

【答案】解：（Ⅰ）令a=b=1，可得2f（1）=f（1），
解得f（1）=0；
令a=b=2，可得2f（2）=f（4）=﹣2，
令a=4，b= ，可得f（4）+f（ ）=f（1）=0，
即有f（ ）=﹣f（4）=2；
（Ⅱ）证明：设x1 ， x2∈（0，+∞）且x1＜x2 ，
可得 ＞1，即有f（ ）＜0，
则f（x2）=f（x1 ）=f（x1）+f（ ）＜f（x1），
∴f（x）在（0，+∞）上是减函数；
（Ⅲ）f（log4x）＞2即为
f（log4x）＞ ，
由（Ⅱ）f（x）在（0，+∞）上是减函数
所以 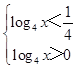，即为 ，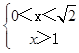
解得 ，
故不等式的解集为（1， ）
【解析】（Ⅰ）令a=b=1，代入计算即可求得f（1）=0；令a=b=2，求得f（4）=﹣2，令a=4，b= ，即可得到所求值；（Ⅱ）运用单调性的定义证明，注意运用条件可得 ＞1，即有f（ ）＜0；（Ⅲ）f（log4x）＞2即为f（log4x）＞ ，由（Ⅱ）f（x）在（0，+∞）上是减函数，可得不等式组，解得即可得到所求集合．