题目内容
11.抛物线$y=\frac{1}{4}{x^2}$上到焦点的距离等于6的点的坐标为$(2\sqrt{5},5),(-2\sqrt{5},5)$.分析 先根据抛物线方程求得焦点坐标及准线方程,进而根据抛物线的定义可知点P到焦点的距离与到准线的距离相等,进而推断出yp+1=6,求得yp,代入抛物线方程即可求得点P的横坐标,则点P的坐标可得.
解答 解:根据抛物线方程可求得焦点坐标为(0,1),准线方程为y=-1,
根据抛物线定义,∴yp+1=6,
解得yp=5,代入抛物线方程求得x=±2$\sqrt{5}$
∴P点坐标是$(2\sqrt{5},5),(-2\sqrt{5},5)$.
故答案为:$(2\sqrt{5},5),(-2\sqrt{5},5)$.
点评 本题主要考查抛物线的定义:抛物线上的点到焦点距离与到准线距离相等,常可用来解决涉及抛物线焦点的直线或焦点弦的问题.

练习册系列答案
相关题目
16.已知奇函数y=f(x)的导函数f′(x)<0在R恒成立,且x,y满足不等式f(x2-2x)+f(y2-2y)≥0,则$\sqrt{{x^2}+{y^2}}$的取值范围是( )
| A. | $[0,2\sqrt{2}]$ | B. | $[0,\sqrt{2}]$ | C. | [1,2] | D. | $[\sqrt{2},2\sqrt{2}]$ |

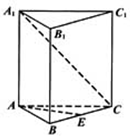 如图,已知正三棱柱ABC-A1B1C1的各棱长均相等,E是BC的中点,点F在侧棱CC1上,且CC1=4CF
如图,已知正三棱柱ABC-A1B1C1的各棱长均相等,E是BC的中点,点F在侧棱CC1上,且CC1=4CF 如图,设A,B分比为椭圆E$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右顶点,P是椭圆E上不同于A,B的一动点,点F是椭圆E的右焦点,直线l是椭圆E的右准线,若直线AP与直线:x=a和l分别相较于C,Q两点,FQ与直线BC交于M.
如图,设A,B分比为椭圆E$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右顶点,P是椭圆E上不同于A,B的一动点,点F是椭圆E的右焦点,直线l是椭圆E的右准线,若直线AP与直线:x=a和l分别相较于C,Q两点,FQ与直线BC交于M.