题目内容
设双曲线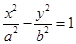
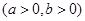 的右焦点为
的右焦点为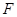 ,过点
,过点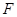 作与
作与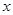 轴垂直的直线
轴垂直的直线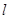 交两渐近线于A,B两点,与双曲线的其中一个交点为
交两渐近线于A,B两点,与双曲线的其中一个交点为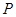 ,设O为坐标原点,若
,设O为坐标原点,若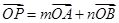 (
(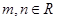 ),且
),且 ,则该双曲线的离心率为( )
,则该双曲线的离心率为( )
A.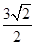 B.
B.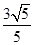 C.
C. 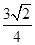 D.
D.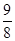
【答案】
C
【解析】
试题分析:双曲线渐近线为y=± ,右焦点为F(c,0),c2=a2+b2,过右焦点与x轴垂直的直线为x=c,与渐近线的交点为A(c,eb), B(c,-eb),与双曲线的交点之一为P(c,b
,右焦点为F(c,0),c2=a2+b2,过右焦点与x轴垂直的直线为x=c,与渐近线的交点为A(c,eb), B(c,-eb),与双曲线的交点之一为P(c,b ),所以
),所以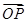 =(c,b
=(c,b ),
), =m(c,eb)=(mc,meb),
=m(c,eb)=(mc,meb), =n(c,-eb)=(nc,-neb),
=n(c,-eb)=(nc,-neb),
因为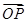 =
= +
+ ,所以(c,b
,所以(c,b )=(mc,meb)+(nc,-neb),即(c,b
)=(mc,meb)+(nc,-neb),即(c,b )=(mc+nc,meb-neb),所以m+n=1,且(m-n)e=
)=(mc+nc,meb-neb),所以m+n=1,且(m-n)e= ,又
,又 ,所以m=
,所以m=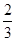 ,n=
,n=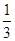 ,代入(m-n)e=
,代入(m-n)e= 中,可解得e=
中,可解得e=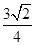 .
.
考点:1.双曲线的性质;2.向量的线性运算;3.方程思想.

练习册系列答案
相关题目
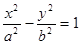
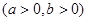 的右焦点为
的右焦点为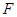 ,过点
,过点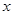 轴垂直的直线
轴垂直的直线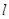 交两渐近线于A,B两点,与双曲线的其中一个交点为
交两渐近线于A,B两点,与双曲线的其中一个交点为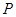 ,设O为坐标原点,若
,设O为坐标原点,若 (
(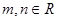 ),且
),且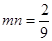 ,则该双曲线的离心率为
,则该双曲线的离心率为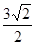 B.
B.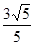 C.
C.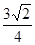 D.
D.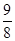
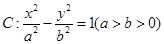 的右焦点为
的右焦点为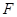 ,左右顶点分别为
,左右顶点分别为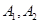 ,过
,过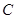 的一条渐近线平行的直线
的一条渐近线平行的直线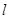 与另一条渐近线相交于
与另一条渐近线相交于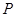 ,若
,若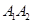 为直径的圆上,则双曲线的离心率为________
______.
为直径的圆上,则双曲线的离心率为________
______. 的右焦点为F,右准线
的右焦点为F,右准线 与两条渐近线交于P,Q两点,如果
与两条渐近线交于P,Q两点,如果 是直角三角形,则双曲线的离心率为 (
)
是直角三角形,则双曲线的离心率为 (
) C.
C.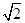 D.
D.