题目内容
(本小题满分12分)
在平面直角坐标系中,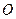 为坐标原点,
为坐标原点,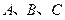 三点满足
三点满足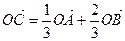
(Ⅰ)求证: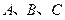 三点共线;
三点共线;
(Ⅱ)求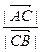 的值;
的值;
(Ⅲ )已知
)已知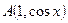 、
、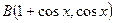 ,
,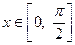
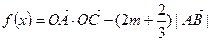 的最小值为
的最小值为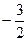 ,求实
,求实 数
数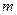 的值.
的值.
解:(Ⅰ)由已知 ,即
,即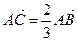 ,
,
∴
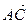 ∥
∥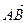 . 又∵
. 又∵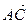 、
、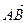 有公共点
有公共点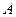 ,∴
,∴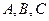 三点共线.------3分
三点共线.------3分
(Ⅱ)∵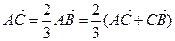 ,∴
,∴
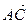 =
=
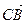 ∴
∴ ,∴
,∴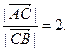
------6分
(Ⅲ)∵C为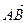 的定比分点,
的定比分点,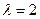 ,∴
,∴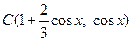 ,
,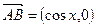
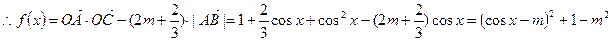 ∵
∵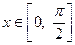 ,∴
,∴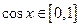 -----------8分
-----------8分
当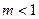 时,当
时,当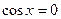 时,
时,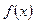 取最小值
取最小值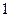 与已知相矛盾;---9分
与已知相矛盾;---9分
当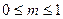 时, 当
时, 当 时,
时,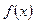 取最小值
取最小值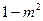 ,得
,得 (舍) –--10分
(舍) –--10分
当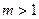 时,当
时,当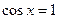 时,
时,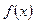 取得最小值
取得最小值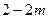 ,得
,得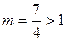 ---11分
---11分
综上所述, 为所求.--------12分
为所求.--------12分
解析

练习册系列答案
相关题目