题目内容
13.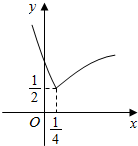 如图所示的函数F(x)的图象是由指数函数f(x)=ax(a>0且a≠1)与幂函数g(x)=xa“拼接“而成的,则下列四个数中最大的是( )
如图所示的函数F(x)的图象是由指数函数f(x)=ax(a>0且a≠1)与幂函数g(x)=xa“拼接“而成的,则下列四个数中最大的是( )| A. | aa | B. | aα | C. | αα | D. | αa |
分析 根据图象过点($\frac{1}{4}$,$\frac{1}{2}$),求出a=$\frac{1}{16}$,α=$\frac{1}{2}$,再根据指数函数和幂函数的图象比较即可.
解答 解:由指数函数的图象和幂函数的图象和已知的图可知,图象均过点($\frac{1}{4}$,$\frac{1}{2}$),
∴f($\frac{1}{4}$)=${a}^{\frac{1}{4}}$=$\frac{1}{2}$,g($\frac{1}{4}$)=$(\frac{1}{4})^{α}$=$\frac{1}{2}$
解得a=$\frac{1}{16}$,α=$\frac{1}{2}$,
∴aa>aα,αa>αα,aα<αα,aa<αa,
∴αa最大,
故选:D.
点评 本题考查了指数函数和幂函数图象和性质,关键是求出a和α,属于基础题.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
1.若α=-4,则角α是( )
| A. | 第一象限角 | B. | 第二象限角 | C. | 第三象限角 | D. | 第四象限角 |
3.已知点A(2,-3),B(-3,-2)直线l过点P(1,1),且与线段AB相交,则直线l的斜率k的取值范围是( )
| A. | $(-∞,-4]∪[\frac{3}{4},+∞)$ | B. | $(-∞,-\frac{1}{4}]∪[\frac{3}{4},+∞)$ | C. | $[-4,\frac{3}{4}]$ | D. | $[\frac{3}{4},4]$ |