��Ŀ����
(��С������12��)��ע�⣺���������������Ч)
Ͷ��ij��־�ĸ����������λ����ר�ҽ�����������ͨ����λ����ר�ҵ�����
������¼�ã�����λ����ר�Ҷ�δ��ͨ��������¼�ã���ǡ��ͨ��һλ����ר�ҵ���
�������ɵ���λר�ҽ��и�������ͨ������ר�ҵ�����������¼�ã�������¼
�ã�������ͨ��������ר������ĸ��ʾ�Ϊ0��5������ĸ����ͨ������ĸ���Ϊ0��3��
��ר�Ҷ�������
��I����Ͷ������־��1ƪ�����¼�õĸ��ʣ�
��II����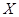 ��ʾͶ������־��4ƪ����б�¼�õ�ƪ������
��ʾͶ������־��4ƪ����б�¼�õ�ƪ������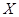 �ķֲ��м�������
�ķֲ��м�������
��I��0.40.
��II���ֲ��м�������
��������������Ҫ����������¼��ĸ��ʡ���ɢ����������ķֲ������������Լ�������˼ά����������������ͬʱ����������۵�˼�롢ת���뻯���˼��.
(��)�� A��ʾ�¼��������ͨ����λ����ר�ҵ�����
B��ʾ�¼������ǡ��ͨ��һλ����ר�ҵ�����
C��ʾ�¼��������ͨ������ר�ҵ�����
D��ʾ�¼��������¼��.
�� D=A+B��C,


=
=
=0.25+0.5��0.3
=0.40.
(��) ����ֲ���Ϊ��
����ֲ���Ϊ��





���� .
.
����������������֪�����¼��ĸ��������㸴���¼��ĸ��ʼ����������ɢ��������ķֲ��������������Ǹ߿��Ը�����ͳ�Ƶ�һ�ֳ���������ȥ��Ҳ��ͬ���Ŀ���. �߿��Ը�����ͳ�ƻ�����һ�ֳ����������������������¼��ĸ��ʣ�������Ҫ��������������ϵ�֪ʶ��ȷ���������¼��ĸ��ʣ�Ȼ���ټ�������¼��ĸ��ʡ���ɢ��������ķֲ���������.
