题目内容
(本小题满分12分)已知椭圆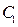 的方程为
的方程为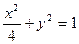 ,双曲线
,双曲线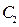 的左、右焦
的左、右焦
点分别是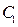 的左、右顶点,而
的左、右顶点,而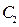 的左、右顶点分别是
的左、右顶点分别是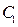 的左、右焦点.
的左、右焦点.
(1)求双曲线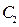 的方程;
的方程;
(2)若直线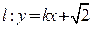 与双曲线C2恒有两个不同的交点A和B,求
与双曲线C2恒有两个不同的交点A和B,求 的范围。
的范围。
解:(1)设双曲线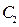 的方程为
的方程为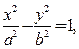 …… 1分,
…… 1分,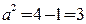 ,再由
,再由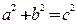 得
得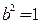 ,………3分,
,………3分,
故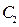 的方程为
的方程为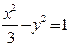 ……………5分
……………5分
(2)将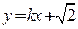 代入
代入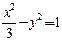 得
得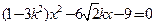 ………6分
………6分
由直线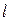 与双曲线C2交于不同的两点得:
与双曲线C2交于不同的两点得: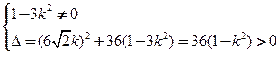 ……8分
……8分
则由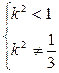 ……………9分解得:
……………9分解得: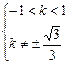 ……………11分
……………11分
故k的取值范围为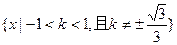 . ……………12分
. ……………12分
解析

练习册系列答案
相关题目
已知椭圆 、抛物线
、抛物线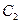 的焦点均在
的焦点均在 轴上,
轴上, 的中心和
的中心和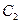 的顶点均为原点
的顶点均为原点 ,从每条曲线上取两个点,将其坐标记录于下表中:
,从每条曲线上取两个点,将其坐标记录于下表中:
 | 3 |  2 2 | 4 |  |
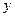 |  | 0 |  4 4 |  |
 的标准方程;
的标准方程;(Ⅱ)请问是否存在直线
 满足条件:①过
满足条件:①过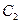 的焦点
的焦点 ;②与
;②与 交不同两点
交不同两点 且满足
且满足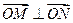 ?若存在,求出直线
?若存在,求出直线 的方程;若不存在,说明理由.
的方程;若不存在,说明理由. 在极坐标系中,以极点为坐标原点,极轴为x轴正半轴,建立直角坐标系,点M(2, )的直角坐标是( )
)的直角坐标是( )
| A.(2,1) | B.( ,1) ,1) | C.(1, ) ) | D.(1,2) |
极坐标方程ρ=cosθ和参数方程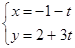 (t为参数)所表示的图形分别为( )
(t为参数)所表示的图形分别为( )
| A.圆、直线 | B.直线、圆 | C.圆、圆 | D.直线、直线 |
在极坐标系中与圆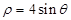 相切的一条直线的方程为( )
相切的一条直线的方程为( )
A.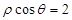 | B.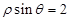 | C.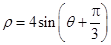 | D.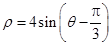 |
极坐标方程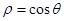 和参数方程
和参数方程 (
( 为参数)所表示的图形分别是
为参数)所表示的图形分别是
| A.圆、直线 | B.直线、圆 | C.圆、圆 | D.直线、直线 |
 ,记点P的轨迹为E.
,记点P的轨迹为E.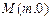 ,使
,使 恒成立,求实数m的值.
恒成立,求实数m的值. 相交于A、B两点。
相交于A、B两点。 ,焦距为2,求椭圆的标准方程;
,焦距为2,求椭圆的标准方程; (其中O为坐标原点),当椭圆的离率
(其中O为坐标原点),当椭圆的离率 时,求椭圆的长轴长的最大值。
时,求椭圆的长轴长的最大值。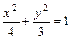 ,在曲线C上是否存在不同两点A、B关于直线
,在曲线C上是否存在不同两点A、B关于直线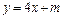 (m为常数)对称?若存在,求出
(m为常数)对称?若存在,求出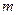 满足的条件;若不存在,说明理由。
满足的条件;若不存在,说明理由。