题目内容
函数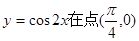 处的切线方程是( )
处的切线方程是( )
A.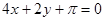 | B.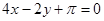 |
C.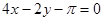 | D.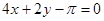 |
D
解析试题分析:根据导数的性质,函数在某点处的切线的斜率就是函数在该点处的导数.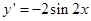 ,因此所求切线的斜率为
,因此所求切线的斜率为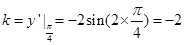 ,故切线方程为
,故切线方程为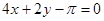
考点:导数与切线方程.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设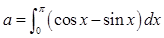 ,则二项式
,则二项式 展开式中的
展开式中的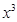 项的系数为( )
项的系数为( )
| A.20 | B.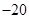 | C.160 | D. |
已知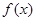 为R上的可导函数,且
为R上的可导函数,且 ,均有
,均有 ,则有 ( )
,则有 ( )
A. 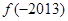 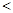 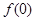 , ,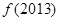 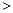  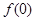 |
B. 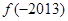 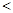 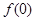 , ,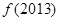 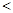  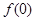 |
C. 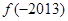 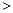 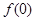 , ,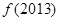 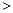  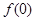 |
D. 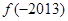 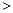 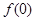 , ,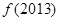 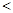  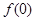 。 。 |
已知曲线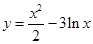 的一条切线的斜率为2,则切点的横坐标为( )
的一条切线的斜率为2,则切点的横坐标为( )
| A.3 | B.2 | C.1 | D. |
从如图所示的正方形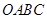 区域内任取一个点
区域内任取一个点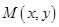 ,则点
,则点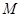 取自阴影部分的概率为( )
取自阴影部分的概率为( )
A.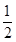 | B.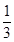 | C.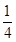 | D.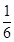 |
设函数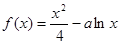 ,若
,若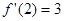 则
则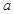 的值为( )
的值为( )
A.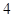 | B.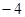 | C.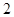 | D.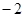 |
在弹性限度内,弹簧所受的压缩力 与缩短的距离
与缩短的距离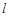 按 胡克定律
按 胡克定律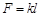 计算.今有一弹簧原长
计算.今有一弹簧原长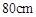 ,每压缩
,每压缩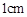 需
需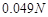 的压缩力,若把这根弹簧从
的压缩力,若把这根弹簧从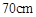 压缩至
压缩至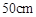 (在弹性限度内),外力克服弹簧的弹力做了( )功(单位:
(在弹性限度内),外力克服弹簧的弹力做了( )功(单位: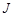 )
)
A.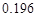 | B. | C.0.686 | D.0.98 |
由直线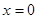 ,
,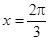 ,
,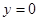 与曲线
与曲线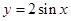 所围成的图形的面积等于( )
所围成的图形的面积等于( )
A.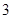 | B.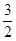 | C.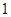 | D.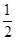 |
 、
、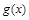 都是定义在R上的函数,
都是定义在R上的函数,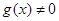 ,
,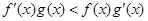 ,
, ,
, ,则关于
,则关于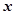 的方程
的方程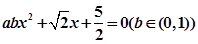 有两个不同实根的概率为( )
有两个不同实根的概率为( )