题目内容
如图,正方形ABCD的边长为2,PA⊥平面ABCD,DE∥PA,且PA=2DE=2,F是PC的中点.(1)求证:EF∥平面ABCD;
(2)求点A到平面PCE的距离;
(3)求平面PCE与面ABCD所成锐二面角的余弦值.

【答案】分析:(1)要证明EF∥平面ABCD,关键是要在平面ABCD中找到一条与EF平行的直线,我们不妨AC∩BD=O,连接OF,则易证ODEF为平行四边形,进而得到EF∥OD,然后根据线面平行的判定定理即可得到结论.
(2)由已知条件,我们易得到平面PCE⊥平面PAC,则过A点做PC的垂线,垂足为H,则AH即为点A到平面PCE的距离,解△PAC,易得结果.
(3)延长PE与AD交于点G,则CG即为两面角的棱,注意到PA=2DE=2,F是PC的中点,我们易得GC⊥PC,且GC⊥AC,则∠PCA为二面角P-CG-A的平面角,解三角形PAC即可得到结论.
解答: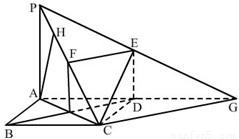 解:(1)设AC∩BD=O,连接OF,
解:(1)设AC∩BD=O,连接OF,
则OF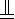
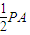
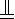 DE,
DE,
∴ODEF为平行四边形.
故EF∥平面ABCD.
(2)∵PA⊥平面ABCD,
∴PA⊥BD.
又AC⊥BD,∴BD⊥平面PAC.
∵EF∥BD,∴EF⊥平面PAC.
又EF?平面PCE,∴平面PCE⊥平面PAC.
作AH⊥PC,垂足为H,则AH⊥平面PCE.
∴AH为点A到平面PCE的距离
在Rt△PAC中,
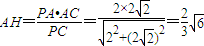 .
.
∴点A到平面PCE的距离为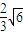 .
.
(3)设PE∩AD=G,连接CG.∵PA=2DE,
∴AD=DG,从而CG∥BD,又BD⊥平面PAC,∴CG⊥平面PAC.
∴∠PCA为二面角P-CG-A的平面角.
在Rt△PAC中, ,
,
∴平面PCE与面ABCD所成锐二面角的余弦值为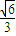 .
.
点评:求二面角的大小,一般先作出二面角的平面角.此题是利用二面角的平面角的定义作出∠PCA为二面角P-CG-A的平面角,通过解∠PCA所在的三角形求得∠PCA.其解题过程为:作∠PCA→证∠PCA是二面角的平面角→计算∠PCA,简记为“作、证、算”.
(2)由已知条件,我们易得到平面PCE⊥平面PAC,则过A点做PC的垂线,垂足为H,则AH即为点A到平面PCE的距离,解△PAC,易得结果.
(3)延长PE与AD交于点G,则CG即为两面角的棱,注意到PA=2DE=2,F是PC的中点,我们易得GC⊥PC,且GC⊥AC,则∠PCA为二面角P-CG-A的平面角,解三角形PAC即可得到结论.
解答:
 解:(1)设AC∩BD=O,连接OF,
解:(1)设AC∩BD=O,连接OF,则OF
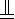
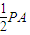
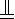 DE,
DE,∴ODEF为平行四边形.
故EF∥平面ABCD.
(2)∵PA⊥平面ABCD,
∴PA⊥BD.
又AC⊥BD,∴BD⊥平面PAC.
∵EF∥BD,∴EF⊥平面PAC.
又EF?平面PCE,∴平面PCE⊥平面PAC.
作AH⊥PC,垂足为H,则AH⊥平面PCE.
∴AH为点A到平面PCE的距离
在Rt△PAC中,
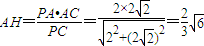 .
.∴点A到平面PCE的距离为
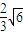 .
.(3)设PE∩AD=G,连接CG.∵PA=2DE,
∴AD=DG,从而CG∥BD,又BD⊥平面PAC,∴CG⊥平面PAC.
∴∠PCA为二面角P-CG-A的平面角.
在Rt△PAC中,
 ,
,∴平面PCE与面ABCD所成锐二面角的余弦值为
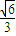 .
.点评:求二面角的大小,一般先作出二面角的平面角.此题是利用二面角的平面角的定义作出∠PCA为二面角P-CG-A的平面角,通过解∠PCA所在的三角形求得∠PCA.其解题过程为:作∠PCA→证∠PCA是二面角的平面角→计算∠PCA,简记为“作、证、算”.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,AB=
如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,AB= 8、如图把正方形ABCD沿对角线BD折成直二面角,对于下面结论:
8、如图把正方形ABCD沿对角线BD折成直二面角,对于下面结论: 如图,正方形ABCD、ABEF的边长都是1,而且平面ABCD、ABEF互相垂直,点M在AC上移动,点N在BF上移动,若CM=BN=a(0<a<
如图,正方形ABCD、ABEF的边长都是1,而且平面ABCD、ABEF互相垂直,点M在AC上移动,点N在BF上移动,若CM=BN=a(0<a< 如图,正方形ABCD所在平面与等腰三角形EAD所在平面相交于AD,AE⊥平面CDE.
如图,正方形ABCD所在平面与等腰三角形EAD所在平面相交于AD,AE⊥平面CDE. (2010•温州二模)如图,正方形ABCD与正方形CDEF所成的二面角为60°,则直线EC与直线AD所成的角的余弦值为
(2010•温州二模)如图,正方形ABCD与正方形CDEF所成的二面角为60°,则直线EC与直线AD所成的角的余弦值为