题目内容
如图,三棱锥P-ABC中,PC 平面ABC,PC=AC=2, AB=BC,D是PB上一点,且CD
平面ABC,PC=AC=2, AB=BC,D是PB上一点,且CD 平面PAB
平面PAB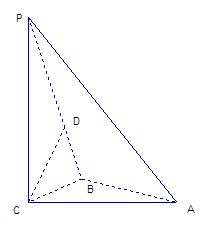
(1)求证:AB 平面PCB;
平面PCB;
(2)求异面直线AP与BC所成角的大小;
(3)求二面角C-PA-B 的大小的余弦值。
(1)根据题意,由于PC 平面ABC,AB
平面ABC,AB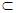 平面ABC,
平面ABC,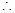 PC
PC AB,同时
AB,同时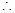 CD
CD  AB,然后得证明。
AB,然后得证明。
(2)建立空间直角坐标系来分析平面的法向量以及直线 方向向量来求解线面角
(3) 
解析试题分析:解:(1)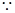 PC
PC 平面ABC,AB
平面ABC,AB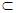 平面ABC,
平面ABC,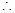 PC
PC AB,
AB,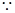 CD
CD 平面PAB,AB
平面PAB,AB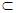 平面PAB,
平面PAB, 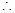 CD
CD  AB。又
AB。又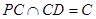 ,
,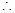 AB
AB  平面PCB
平面PCB
(2)由(1)AB  平面PCB ,
平面PCB , PC=AC=2, 又
PC=AC=2, 又 AB=BC, 可求得BC=
AB=BC, 可求得BC= 
以B为原点,如图建立空间直角坐标系,
则A(0, ,0),B(0,0,0), C(
,0),B(0,0,0), C( ,0,0) P(
,0,0) P( ,0,2)
,0,2)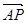 =(
=( ,-
,- ,2),
,2),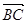 =(
=( ,0,0) 则
,0,0) 则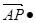
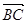 =
=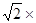
 +0+0=2
+0+0=2
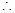 异面直线AP与BC所成的角为
异面直线AP与BC所成的角为
(3)设平面PAB的法向量为m=(x,y,z)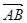 =(0,-
=(0,- ,0),
,0),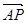 =(
=( ,
,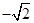 ,2)
,2)
则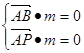 ,即,得m=(
,即,得m=( ,0,-1)设平面PAC的法向量为n=(x,y,z)
,0,-1)设平面PAC的法向量为n=(x,y,z)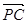 =(0,0,-2),
=(0,0,-2),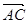 =(
=( ,-
,- ,0),则
,0),则
得n=(1,1,0)cos<m,n>=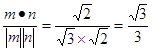
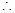 二面角C-PA-B大小的余弦值为
二面角C-PA-B大小的余弦值为
考点:空间中点线面 位置关系的运用
点评:解决该试题的关键是能熟练的运用线面垂直判定定理来证明,以及向量法求解角的问题,属于基础题。

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案
相关题目
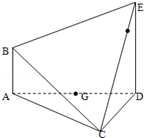
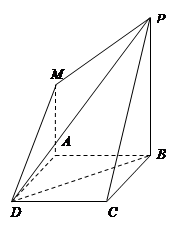
 中,
中, 底面
底面 ,
,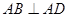 ,
,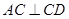 ,
,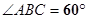 ,
,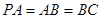 ,
,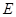 是
是 的中点.
的中点.
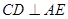 ;
; 平面
平面 ;
; 的余弦值.
的余弦值.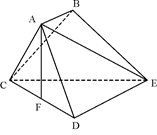
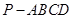 中
中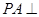 平面
平面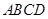 ,
,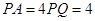 ,底面为直角梯形,
,底面为直角梯形,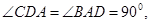
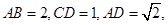
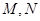 分别是
分别是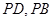 的中点.
的中点.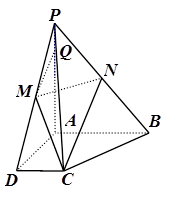
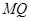 // 平面
// 平面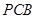 ;
;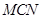 与底面
与底面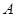 到平面
到平面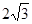 , BC=6.
, BC=6.
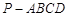 中,底面
中,底面 是边长为2的菱形,
是边长为2的菱形,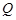 是棱
是棱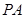 上的动点.
上的动点.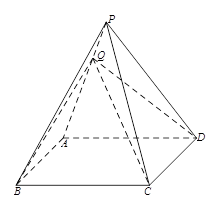
 是
是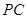 //平面
//平面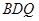 ;
;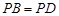 ,求证:
,求证: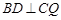 ;
;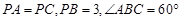 ,求四棱锥
,求四棱锥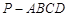 的底面
的底面 为菱形,
为菱形,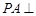 平面
平面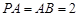 , E、F分别为
, E、F分别为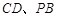 的中点,
的中点,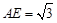 .
.
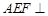 平面
平面 .
. 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.