题目内容
【题目】如图,楔形几何体![]() 由一个三棱柱截去部分后所得,底面
由一个三棱柱截去部分后所得,底面![]() 侧面
侧面![]() ,
,![]() ,楔面
,楔面![]() 是边长为2的正三角形,点
是边长为2的正三角形,点![]() 在侧面
在侧面![]() 的射影是矩形
的射影是矩形![]() 的中心
的中心![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() .
.
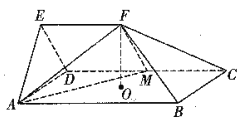
(1)证明:![]() 平面
平面![]() ;
;
(2)求楔形几何体![]() 的体积.
的体积.
【答案】(1)证明见解析(2)![]()
【解析】
(1)连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,
,![]() ,则
,则![]() 是
是![]() 的中点,
的中点,![]() ,利用线段的度量计算证明
,利用线段的度量计算证明![]() ,
,![]() 即可得答案;
即可得答案;
(2)由(1)可知,楔形几何体![]() 由直三棱柱
由直三棱柱![]() 和四棱锥
和四棱锥![]() 组成,利用柱体和锥体的体积公式计算即可.
组成,利用柱体和锥体的体积公式计算即可.
(1)如图,连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,
,![]() .
.
则![]() 是
是![]() 的中点,
的中点,![]() .
.
因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ,
,
又平面![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ,
,
根据题意,四边形![]() 和
和![]() 是全等的直角梯形,
是全等的直角梯形,
三角形![]() 和
和![]() 是全等的等腰直角三角形,
是全等的等腰直角三角形,
所以![]() ,
,![]() ,
,
在直角三角形![]() 中,
中,![]() ,
,
所以![]() ,
,![]() ,
,![]() .
.
于是![]() ,
,![]() ,所以
,所以![]() ,
,![]() .
.
因为![]() 平面
平面![]() ,
,![]() ,
,
所以![]() 平面
平面![]() .
.

(2)由(1)可知,楔形几何体![]() 由直三棱柱
由直三棱柱![]() 和四棱锥
和四棱锥![]() 组成,
组成,
直三棱柱![]() 的体积为
的体积为![]()
![]() ,
,
四棱锥![]() 的体积为
的体积为![]()
![]() ,
,
所以楔形几何体![]() 的体积为
的体积为![]() .
.

练习册系列答案
相关题目
【题目】十三届全国人大二次会议于2019年3月5日在京召开为了了解某校大学生对两会的关注程度,学校媒体在开幕后的第二天,从全校学生中随机抽取了180人,对是否收看2019年两会开幕会情况进行了问卷调查,统计数据如下:
收看 | 没收看 | |
男生 | 80 | 40 |
女生 | 30 | 30 |
(1)根据上表说明,在犯错误的概率不超过1%的前提下,能否认为该校大学生收看开幕会与性别有关?(计算结果精确到0.001)
(2)现从随机抽取的学生中,采用按性别分层抽样的方法选取6人,来参加2019年两会的志愿者宣传活动,若从这6人中随机选取2人到各班级宣传介绍,求恰好选到一名男生和一名女生的概率. 附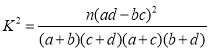 ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.025 | 0.01 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |