题目内容
把1、3、6、10、15、21、…这些数叫做三角形数,这是因为这些数目的点子可以排成一个正三角形(如图),试求第七个三角形数是( )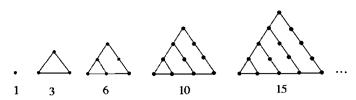
| A.27 | B.28 | C.29 | D.30 |
B
解析试题分析:解:原来三角形数是从l开始的连续自然数的和. l是第一个三角形数, 3是第二个三角形数, 6是第三个三角形数, 10是第四个三角形数, 15是第五个三角形数,…那么,第七个三角形数就是:l+2+3+4+5+6+7=28.故选B
考点:数列
点评:本题考查数列在生产实际中的应用,考查运算求解能力,推理论证能力;考查化归与转化思想.综合性强,难度大,易出错,是高考的重点.解题时要认真审题,注意总结规律

练习册系列答案
相关题目
用反证法证明命题:若整系数一元二次方程 有有理数根,那么
有有理数根,那么 中至少有一个是偶数,下列假设中正确的是 ( )
中至少有一个是偶数,下列假设中正确的是 ( )
A.假设 都是偶数 都是偶数 | B.假设 都不是偶数 都不是偶数 |
C.假设 至多有一个偶数 至多有一个偶数 | D.假设 至多有两个偶数 至多有两个偶数 |
用反证法证明命题“设a,b∈R,|a|+|b|<1,a2-4b≥0,那么x2+ax+b=0的两根的绝对值都小于1”时,应假设
| A.方程x2+ax+b=0的两根的绝对值存在一个小于1 |
| B.方程x2+ax+b=0的两根的绝对值至少有一个大于等于1 |
| C.方程x2+ax+b=0没有实数根 |
| D.方程x2+ax+b=0的两根的绝对值都不小于1 |
用反证法证明“如果a>b,那么 >
> ”假设的内容应是( )
”假设的内容应是( )
A. = = | B. < < |
C. = = 且 且 < < | D. = = 或 或 < < |
用数学归纳法证明不等式1+ +
+ +…+
+…+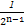 >
>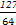 (n∈N*)成立,其初始值至少应取( )
(n∈N*)成立,其初始值至少应取( )
| A.7 | B.8 | C.9 | D.10 |
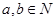 ,
,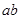 可被
可被 整除,那么
整除,那么 中至少有一个能被
中至少有一个能被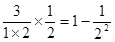 ; ?
; ? ;
; ,
, 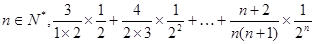 = .
= .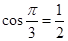


 +
+ +…+
+…+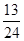 的过程中,由n=k推导n=k+1时,不等式的左边增加的式子是________.
的过程中,由n=k推导n=k+1时,不等式的左边增加的式子是________.