题目内容
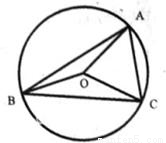
如图,在△ABC中;角A、B、C所对的边分别是a、b、c,且a=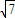 ,b=2,c=3,O为△ABC的外心.
,b=2,c=3,O为△ABC的外心.(I)求△ABC的面积;
(II)求
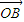 •
•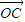 .
.
【答案】分析:(I)在△ABC中,由余弦定理可得 cosA 的值,即 A 的值,从而得到△ABC的面积为  的值.
的值.
(II)∠BOC=2∠BAC=120°,由正弦定理可得 r,由 •
•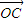 =|OB|•|OC|cos∠BOC=
=|OB|•|OC|cos∠BOC=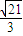 •
•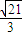 cos120°,求得结果.
cos120°,求得结果.
解答:解:(I)在△ABC中,由余弦定理可得 cosA= =
= ,∴A=60°,
,∴A=60°,
故△ABC的面积为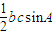 =
=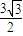 .
.
(II)∵∠BOC=2∠BAC=120°,由正弦定理可得 2r=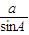 =
=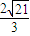 ,∴r=
,∴r=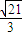 ,
,
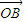 •
•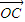 =|OB|•|OC|cos∠BOC=
=|OB|•|OC|cos∠BOC= •
• cos120°=-
cos120°=- .
.
点评:本题考查正弦定理、余弦定理的应用,两个向量的数量积的定义,求出△ABC 的外接圆半径r,是解题的关键.
 的值.
的值.(II)∠BOC=2∠BAC=120°,由正弦定理可得 r,由
 •
•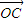 =|OB|•|OC|cos∠BOC=
=|OB|•|OC|cos∠BOC=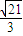 •
•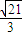 cos120°,求得结果.
cos120°,求得结果.解答:解:(I)在△ABC中,由余弦定理可得 cosA=
 =
= ,∴A=60°,
,∴A=60°,故△ABC的面积为
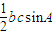 =
=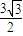 .
.(II)∵∠BOC=2∠BAC=120°,由正弦定理可得 2r=
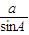 =
=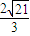 ,∴r=
,∴r=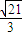 ,
,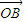 •
•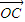 =|OB|•|OC|cos∠BOC=
=|OB|•|OC|cos∠BOC= •
• cos120°=-
cos120°=- .
.点评:本题考查正弦定理、余弦定理的应用,两个向量的数量积的定义,求出△ABC 的外接圆半径r,是解题的关键.

练习册系列答案
相关题目
 如图,在△ABC中,D是边AC上的点,且AB=AD,2AB=
如图,在△ABC中,D是边AC上的点,且AB=AD,2AB=| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在△ABC中,已知∠ABC=90°,AB上一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2cm,
如图,在△ABC中,已知∠ABC=90°,AB上一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2cm, 如图,在△ABC中,设
如图,在△ABC中,设 如图,在△ABC中,∠B=45°,D是BC边上的一点,AD=5,AC=7,DC=3.
如图,在△ABC中,∠B=45°,D是BC边上的一点,AD=5,AC=7,DC=3. 如图,在△ABC中,已知
如图,在△ABC中,已知