题目内容
【题目】已知函数
，（其中
为
在点
处的导数， 
为常数).
（1）求
的值；
（2）求函数
的单调区间；
（3）设函数
，若函数
在区间
上单调递增，求实数
的取值范围。
【答案】（1）
（2）
【解析】试题分析: (1)对
求导,令
,即可求出
;(2)将
代入
中,求导后,分别令
,求出
的范围,得到单调增区间,减区间;(3)由已知有
恒成立,且
,得出
,令
,由
,求出
的范围.
试题解析:（1）
（2）
当
，即
或
时，函数
单调递增；
当
，即
时，函数
单调递减。
∴
单调递增区间为
和
单调递减区间为
（3）
∵
在区间
上单调递增，
∴
恒成立.
∵
∴
设
则
， ∴
， ∴
答： 
的取值范围是
.
点睛:本题主要考查了导数的计算,导数在求函数单调性上的应用,属于中档题.求函数在某区间为增函数,一般转化为导函数大于或等于零问题.第三问另解: 得出
恒成立, 
,分离出常数
,即
,当
时, 
有最大值为11.所以
.
练习册系列答案
相关题目
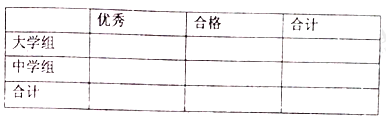
【题目】在一次抽样调查中测得样本的6组数据，得到一个变量
关于
的回归方程模型，其对应的数值如下表：
| 2 | 3 | 4 | 5 | 6 | 7 |
|
|
|
|
|
|
|
(1)请用相关系数
加以说明与之间存在线性相关关系(当
时，说明与之间具有线性相关关系)；
(2)根据(1)的判断结果，建立关于的回归方程并预测当
时，对应的值为多少(
精确到
).
附参考公式：回归方程
中斜率和截距的最小二乘法估计公式分别为：
，
，相关系数公式为：
.
参考数据：
，
，
，
.
