题目内容
已知函数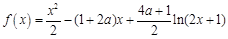 .
.
(1)设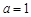 时,求函数
时,求函数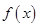 极大值和极小值;
极大值和极小值;
(2)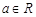 时讨论函数
时讨论函数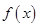 的单调区间.
的单调区间.
【答案】
(1)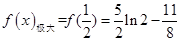 ,
, 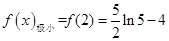
(2)
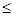
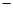
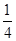 时,
时,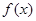 的增区间为(
的增区间为( ,+
,+ ),减区间为(
),减区间为(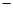
 ,
, )
)
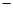
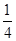 <
< <
<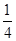 时,
时,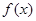 的增区间为(
的增区间为(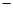
 ,2
,2 )和(
)和( ,+
,+ ),减区间为(2
),减区间为(2 ,
, )
)
 =
=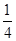 时,
时,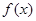 的增区间为(
的增区间为(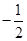 ,+
,+ )
)
 >
>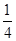 时,
时,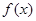 的增区间为(
的增区间为(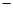
 ,
, )和(2
)和(2 ,+
,+ ),减区间为(
),减区间为( ,2
,2 )
)
【解析】
试题分析:解:(1)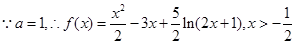 1分
1分
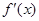 =
=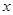
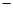 3
3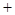
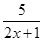 =
=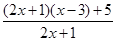 =
=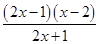 , 2分
, 2分
令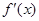 =0,则
=0,则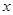 =
= 或
或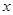 =2
3分
=2
3分
|
|
( |
|
( |
2 |
(2,+ |
|
|
+ |
0 |
|
0 |
+ |
|
|
|
极大 |
|
极小 |
|
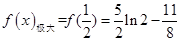 ,
, 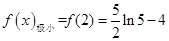 4分
4分
(2)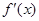 =
=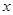
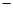 (1+2
(1+2 )+
)+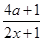 =
= =
=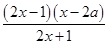
令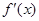 =0,则
=0,则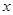 =
= 或
或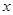 =2
=2 5分
5分
i、当2 >
> ,即
,即 >
>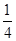 时,
时,
|
|
( |
|
( |
2 |
(2 |
|
|
+ |
0 |
|
0 |
+ |
|
|
|
|
|
|
|
所以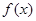 的增区间为(
的增区间为(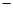
 ,
, )和(2
)和(2 ,+
,+ ),减区间为(
),减区间为( ,2
,2 )
6分
)
6分
ii、当2 =
= ,即
,即 =
=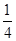 时,
时,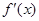 =
=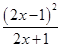
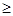 0在(
0在(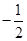 ,+
,+ )上恒成立,
)上恒成立,
所以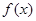 的增区间为(
的增区间为(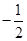 ,+
,+ )
7分
)
7分
iii、当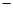
 <2
<2 <
< ,即
,即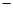
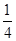 <
< <
<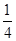 时,
时,
|
|
( |
2 |
(2 |
|
( |
|
|
+ |
0 |
|
0 |
+ |
|
|
|
|
|
|
|
所以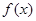 的增区间为(
的增区间为(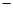
 ,2
,2 )和(
)和( ,+
,+ ),减区间为(2
),减区间为(2 ,
, )
10分
)
10分
iv、当2
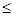
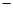
 ,即
,即
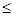
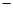
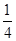 时,
时,
|
|
( |
|
( |
|
|
|
0 |
+ |
|
|
|
|
|
所以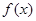 的增区间为(
的增区间为( ,+
,+ ),减区间为(
),减区间为(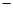
 ,
, ) 12分
) 12分
综上述:

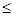
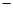
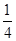 时,
时,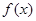 的增区间为(
的增区间为( ,+
,+ ),减区间为(
),减区间为(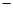
 ,
, )
)
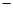
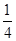 <
< <
<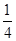 时,
时,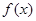 的增区间为(
的增区间为(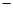
 ,2
,2 )和(
)和( ,+
,+ ),减区间为(2
),减区间为(2 ,
, )
)
 =
=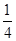 时,
时,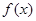 的增区间为(
的增区间为(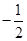 ,+
,+ )
)
 >
>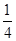 时,
时,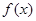 的增区间为(
的增区间为(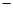
 ,
, )和(2
)和(2 ,+
,+ ),减区间为(
),减区间为( ,2
,2 ). 14分
). 14分
考点:导数的运用
点评:解决的关键是利用导数的符号判定函数单调性,进而确定极值,求解得到。属于基础题。

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目

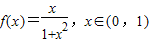 .
. ;
; 的最小值.
的最小值. .
. 的值域.
的值域.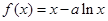 ,
,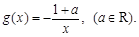
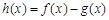 ,求函数
,求函数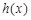 的单调区间;
的单调区间;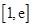 (
(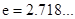 )上存在一点
)上存在一点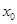 ,使得
,使得
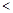
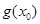 成立,求
成立,求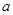 的取值范围.
的取值范围.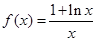 .
.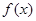 在区间
在区间 上存在极值,求实数a的取值范围;
上存在极值,求实数a的取值范围;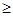 1时,不等式
1时,不等式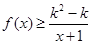 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围. 与
与
 分别相交于点
分别相交于点 ,且曲线
,且曲线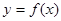 和
和 在点
在点 的值;
的值; 为
为 的导函数,若对于任意的
的导函数,若对于任意的 ,
, 恒成立,求实数
恒成立,求实数 的最大值;
的最大值; 倍时,当
倍时,当 时,若函数
时,若函数 的最小值恰为
的最小值恰为 的最小值,求实数
的最小值,求实数 的值
的值