题目内容
A,B,C是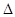 ABC的三个内角,且
ABC的三个内角,且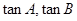 是方程
是方程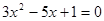 的两个实数根,则
的两个实数根,则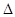 ABC是( )
ABC是( )
| A.等边三角形 | B.锐角三角形 | C.等腰三角形 | D.钝角三角形 |
D
解析试题分析:解:因为tanA,tanB是方程3x2-5x+1=0的两个实根,由韦达定理可得到:tanA+tanB=,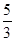 与 tanAtanB=
与 tanAtanB=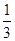 >0,又因为C=π-(A+B),两边去=取正切得到,tanC=
>0,又因为C=π-(A+B),两边去=取正切得到,tanC=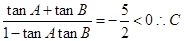 为钝角,即
为钝角,即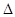 ABC是钝角三角形,选D.
ABC是钝角三角形,选D.
考点:一元二次方程根的分布
点评:此题主要考查一元二次方程根的分布与系数的关系,其中涉及到同角三角函数的正切关系式,属于综合性试题,计算量小为中档题目

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
若 ,则P,Q的大小关系为
,则P,Q的大小关系为
A. | B. | C. | D. |
设 ,则( )
,则( )
A. | B. | C. | D. |
已知 为全集,
为全集, ,则
,则 ( )
( )
A. | B. |
C. | D. |
已知 ,则f(3)为 ( )
,则f(3)为 ( )
| A.2 | B. 3 | C. 4 | D.5 |
函数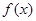 是定义在R上的奇函数,在
是定义在R上的奇函数,在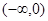 上递增,且
上递增,且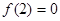 ,则使得
,则使得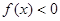 成立的
成立的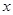 的取值范围是( )
的取值范围是( )
A.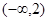 | B.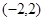 |
C. | D.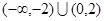 |
已知函数 的两个零点分别在区间
的两个零点分别在区间 和区间
和区间 内,则实数
内,则实数 的取值范围是 ( )
的取值范围是 ( )
A. | B. | C. | D. |
已知 ,且函数
,且函数 恰有3个不同的零点,则实数a的取值范围是
恰有3个不同的零点,则实数a的取值范围是
A.(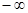 ,l] ,l] | B.(O,1] | C.(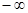 ,O] ,O] | D.(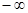 ,2] ,2] |
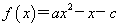 ,且
,且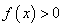 的解集为(-2,1),则函数
的解集为(-2,1),则函数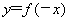 的图象为( )
的图象为( )