题目内容
在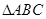 中,
中,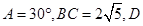 是AB边上的一点,CD=2,
是AB边上的一点,CD=2, 的面积为4,则AC的长为
。
的面积为4,则AC的长为
。
【答案】
.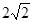 或
或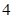
【解析】解:由题意可得1/ 2 CB•CD•sin∠BCD=4,即 1 /2 ×2  ×2 sin∠BCD=4,解得 sin∠BCD=2 /
×2 sin∠BCD=4,解得 sin∠BCD=2 / .
.
①当∠BCD 为锐角时,cos∠BCD=1/ .
.
△BCD中,由余弦定理可得 BD2= CB2+CD2-2•CB•CD•cos∠BCD =42.
△BCD中,由正弦定理可得 BD /sin∠BCD =CD /sinB ,即 4 /2 / = 2 sinB ,故
sinB=1 /
= 2 sinB ,故
sinB=1 / .
.
在△ABC中,由正弦定理可得 AC/ sinB = BC/ sinA ,即 AC /1 / =2
=2  /1
/2 ,解得 AC=4.
/1
/2 ,解得 AC=4.
②当∠BCD 为钝角时,cos∠BCD=-1 / .
.
△BCD中,由余弦定理可得 BD= CB2+CD2-2•CB•CD•cos∠BCD =32.
△BCD中,由正弦定理可得 BD/ sin∠BCD =CD/ sinB ,故 sinB=1 /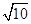 .
.
在△ABC中,由正弦定理可得 AC/ sinB = BC /sinA , ,解得 AC=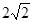 .
.
综上可得 AC=4或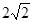 ,
,
故答案为 4或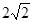 .
.

练习册系列答案
相关题目
 (2013•乐山一模)如图,在三角形ABC中,BE是AC边上的中线,O是BE边的中点,若
(2013•乐山一模)如图,在三角形ABC中,BE是AC边上的中线,O是BE边的中点,若 (2013•湖北)如图,某地质队自水平地面A,B,C三处垂直向地下钻探,自A点向下钻到A1处发现矿藏,再继续下钻到A2处后下面已无矿,从而得到在A处正下方的矿层厚度为A1A2=d1.同样可得在B,C处正下方的矿层厚度分别为B1B2=d2,C1C2=d3,且d1<d2<d3.过AB,AC的中点M,N且与直线AA2平行的平面截多面体A1B1C1-A2B2C2所得的截面DEFG为该多面体的一个中截面,其面积记为S中.
(2013•湖北)如图,某地质队自水平地面A,B,C三处垂直向地下钻探,自A点向下钻到A1处发现矿藏,再继续下钻到A2处后下面已无矿,从而得到在A处正下方的矿层厚度为A1A2=d1.同样可得在B,C处正下方的矿层厚度分别为B1B2=d2,C1C2=d3,且d1<d2<d3.过AB,AC的中点M,N且与直线AA2平行的平面截多面体A1B1C1-A2B2C2所得的截面DEFG为该多面体的一个中截面,其面积记为S中.