题目内容
在直径为AB的半圆形区域内,划出一个三角形区域,使三角形的一边为AB,顶点C在半圆上,其他两边分别为6米和8米.先要建造一个内接于△ABC的矩形水池DEFN,其中,DE在AB上,下图的设计方案是使AC =8米,BC =6米.
图2-5-20
（1）求△ABC的边AB上的高h.
（2）设DN =x,当x取何值时,水池DEFN的面积最大？
（3）实际施工时,发现在AB上距B点1.85米的M处有一棵大树,问:这棵大树是否位于最大矩形水池的边上？如果为保护大树,请设计出另外的方案,使内接于满足条件的三角形中欲建的最大矩形水池能避开大树.
思路分析:（1）利用三角形的面积,即斜边×斜边上的高=两直角边的积;（2）求最值问题时,利用三角形相似得到比例式,转变成二次函数即可.
解:（1）∵直径AB为△ABC的斜边,?
∴AB =
=10米.?
∴h =
=4.8米.?
（2）∵
=
,∴
.?
又∵
=
,?
∴S矩形DEFN?= 
(8-
x)=-
x2+10x =-
.?
∴当
时,S max=12.?
（3）∵BC2=OB·AB,∴OB =3.6米.?
∵
=
,∴BE =1.8米.?
同理,AD =3.2米,?
∴AC =6米,BC =8米即可.
练习册系列答案
相关题目
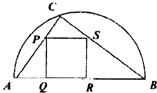如图，某小区准备绿化一块直径为AB的半圆形空地，点C在半圆弧上，半圆内△ABC外的地方种草，△ABC的内接正方形PQRS内部为一水池，其余地方种花，若AB=2a，∠CAB=θ，设△ABC的面积为S1，正方形PQRS的边长为x，面积为S2，将比值
如图，某小区准备绿化一块直径为AB的半圆形空地，点C在半圆弧上，半圆内△ABC外的地方种草，△ABC的内接正方形PQRS内部为一水池，其余地方种花，若AB=2a，∠CAB=θ，设△ABC的面积为S1，正方形PQRS的边长为x，面积为S2，将比值
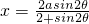称为“规划合理度”．
．
称为“规划合理度”．
．