题目内容
(本小题满分12分)已知数列 各项均不为0,其前
各项均不为0,其前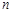 项和为
项和为 ,且对任意
,且对任意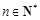 都有
都有 (
(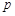 为大于1的常数),记
为大于1的常数),记 .
.
(1) 求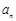 ;
;
(2) 试比较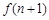 与
与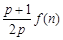 的大小(
的大小(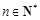 );
);
(3) 求证: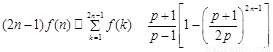
【答案】
(1)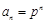 (2)由(1)可得
(2)由(1)可得 ,结合整体思想来得到比较大小
,结合整体思想来得到比较大小
(3)由(2)知 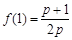 ,
,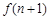
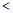
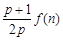 ,(
,(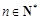 ).结合放缩法来得到证明。
).结合放缩法来得到证明。
【解析】
试题分析:解:(1) ∵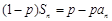 ,① ∴
,① ∴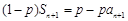 .②
.②
②-①,得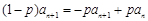 ,即
,即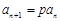 . (3分) 在①中令
. (3分) 在①中令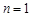 ,
,
可得 .∴
.∴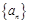 是首项为
是首项为 ,公比为
,公比为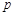 的等比数列,
的等比数列,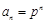 . (4分)
. (4分)
(2) 由(1)可得 .
.

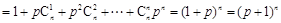 .
.
∴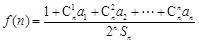
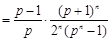 , (5分)
, (5分)
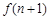
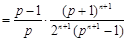 .而
.而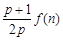
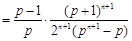 ,且
,且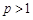 ,
,
∴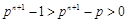 ,
,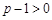 .∴
.∴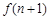
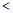
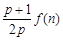 ,(
,(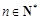 ).(8分)
).(8分)
(3) 由(2)知
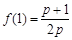 ,
,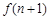
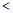
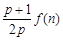 ,(
,(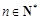 ).
).
∴当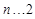 时,
时,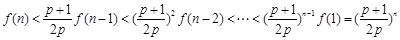 .
.
∴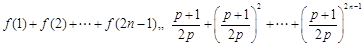
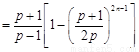 ,(10分)(当且仅当
,(10分)(当且仅当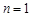 时取等号).
时取等号).
另一方面,当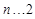 ,
, 时,
时,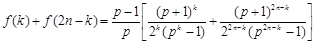
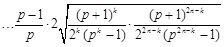
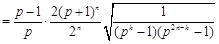
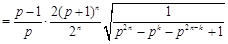 .
.
∵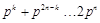 ,∴
,∴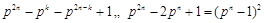 .
.
∴ ,(当且仅当
,(当且仅当 时取等号).(13分)
时取等号).(13分)
∴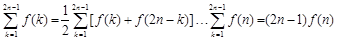 .(当且仅当
.(当且仅当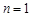 时取等号).
时取等号).
综上所述,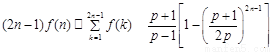 ,(
,(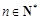 ).(14分)
).(14分)
考点:数列的综合运用
点评:考查了数列的通项公式与前n项和关系的运用,以及能结合已知给定的不等式来放缩法得到证明。

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案
相关题目