题目内容
对于函数 ,给出下列四个结论:①函数f(x)的最小正周期为π;②若f(x1)=-f(x2)则x1=-x2;③f(x)的图象关于直线
,给出下列四个结论:①函数f(x)的最小正周期为π;②若f(x1)=-f(x2)则x1=-x2;③f(x)的图象关于直线 对称;④
对称;④ 上是减函数,其中正确结论的个数为( )
上是减函数,其中正确结论的个数为( )A.2
B.4
C.1
D.3
【答案】分析:根据题意把函数解析式利用诱导公式及二倍角的正弦函数公式化简为f(x)= sin2x,①根据周期公式可得函数周期为π;②可以举例判断其实错误的;③求出函数的所有对称轴可验证得③正确;④求出函数的所有单调减区间可得到④正确,进而得到正确结论的个数.
sin2x,①根据周期公式可得函数周期为π;②可以举例判断其实错误的;③求出函数的所有对称轴可验证得③正确;④求出函数的所有单调减区间可得到④正确,进而得到正确结论的个数.
解答:解:根据题意得:函数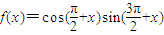 =(-sinα)•(-cosα)=sinαcosα=
=(-sinα)•(-cosα)=sinαcosα= sin2α,
sin2α,
①根据周期公式可得:f(x)= sin2x的周期为π.所以①正确;
sin2x的周期为π.所以①正确;
②f( )=-f(
)=-f( ),但是不满足x1=-x2,所以②错误;
),但是不满足x1=-x2,所以②错误;
③f(x)= sin2x的所有对称轴为x=
sin2x的所有对称轴为x= ,显然③正确;
,显然③正确;
④f(x)= sin2x的单调减区间为[kπ+
sin2x的单调减区间为[kπ+ ,kπ+
,kπ+ ],(k∈Z),显然④正确,
],(k∈Z),显然④正确,
则其中正确结论的个数为3.
故选D
点评:此题考查了正弦函数的单调性及对称性,解决此类问题的关键是灵活利用诱导公式二倍角公式把函数解析式化为一个角的正弦函数,同时要求学生掌握三角函数的有关性质(单调性,周期性,奇偶性,对称性等).
 sin2x,①根据周期公式可得函数周期为π;②可以举例判断其实错误的;③求出函数的所有对称轴可验证得③正确;④求出函数的所有单调减区间可得到④正确,进而得到正确结论的个数.
sin2x,①根据周期公式可得函数周期为π;②可以举例判断其实错误的;③求出函数的所有对称轴可验证得③正确;④求出函数的所有单调减区间可得到④正确,进而得到正确结论的个数.解答:解:根据题意得:函数
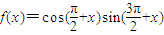 =(-sinα)•(-cosα)=sinαcosα=
=(-sinα)•(-cosα)=sinαcosα= sin2α,
sin2α,①根据周期公式可得:f(x)=
 sin2x的周期为π.所以①正确;
sin2x的周期为π.所以①正确;②f(
 )=-f(
)=-f( ),但是不满足x1=-x2,所以②错误;
),但是不满足x1=-x2,所以②错误;③f(x)=
 sin2x的所有对称轴为x=
sin2x的所有对称轴为x= ,显然③正确;
,显然③正确;④f(x)=
 sin2x的单调减区间为[kπ+
sin2x的单调减区间为[kπ+ ,kπ+
,kπ+ ],(k∈Z),显然④正确,
],(k∈Z),显然④正确,则其中正确结论的个数为3.
故选D
点评:此题考查了正弦函数的单调性及对称性,解决此类问题的关键是灵活利用诱导公式二倍角公式把函数解析式化为一个角的正弦函数,同时要求学生掌握三角函数的有关性质(单调性,周期性,奇偶性,对称性等).

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
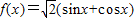 ,给出下列四个命题:
,给出下列四个命题: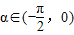 ,使
,使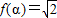 ;
; 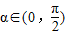 ,使f(x-α)=f(x+α)恒成立;
,使f(x-α)=f(x+α)恒成立;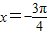 对称;
对称;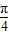 就能得到y=-2cosx的图象
就能得到y=-2cosx的图象 ,给出下列四个结论:①函数
,给出下列四个结论:①函数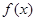 的最小正周期为
的最小正周期为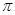 ;②若
;②若 ③
③ 对称;④
对称;④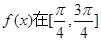 上是减函数,其中正确结论的个数为 ( )
上是减函数,其中正确结论的个数为 ( ) ,给出下列四个命题:
,给出下列四个命题: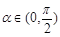 ,使
,使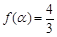 ;
;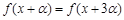 恒成立;
恒成立;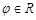 ,使函数
,使函数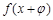 的图象关于y轴对称;
的图象关于y轴对称;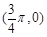 对称.
对称.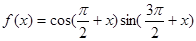 ,给出下列四个结论:①函数
,给出下列四个结论:①函数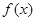 的最小正周期为
的最小正周期为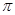 ;②若
;②若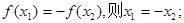 ③
③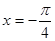 对称;④
对称;④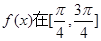 上是减函数,其中正确结论的个数为 ( )
上是减函数,其中正确结论的个数为 ( )