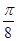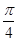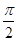题目内容
(2013.淄博一模)在区间 和
和 内分别取一个数,记为
内分别取一个数,记为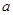 和
和 ,则方程
,则方程 表示离心率小于
表示离心率小于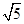 的双曲线的概率为( )
的双曲线的概率为( )
A. | B.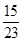 | C.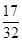 | D.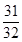 |
B
解析试题分析:由题意可以横轴为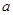 ,纵轴为
,纵轴为 ,建立直角坐标系,先作出满足题意的
,建立直角坐标系,先作出满足题意的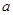 、
、 的可行域
的可行域 ,并求出其面积为
,并求出其面积为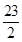 ,又双曲线的离心率小于
,又双曲线的离心率小于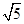 得
得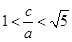 ,则
,则 ,即
,即 ,再作出虚线
,再作出虚线 ,并求出与可行域的端点坐标分别为
,并求出与可行域的端点坐标分别为 、
、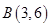 ,由此可求出可行域范围内满足
,由此可求出可行域范围内满足 的面积为
的面积为 ,所以所求概率为
,所以所求概率为 (如图所示).故正确答案为B.
(如图所示).故正确答案为B.
考点:1.线性规划;2.双曲线;3.几何概型.

练习册系列答案
相关题目
若实数x,y满足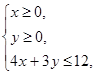 则
则 的取值范围是( )
的取值范围是( )
A.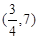 | B.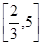 | C.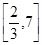 | D.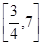 |
若实数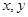 满足
满足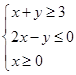 ,则
,则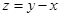 的最小值为 ( )
的最小值为 ( )
A.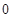 | B. | C.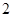 | D.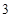 |
若在区间[0,2]中随机地取两个数,则这两个数中较大的数大于 的概率是( )
的概率是( )
A.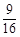 | B.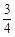 | C.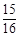 | D.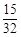 |
已知实数 满足
满足 ,则
,则 的最大值为( )
的最大值为( )
| A.11 | B.12 | C.13 | D.14 |
设变量x,y满足约束条件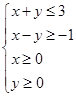 且目标函数z1=2x+3y的最大值为a,目标函数z2=3x-2y的最小值为b,则a+b=( )
且目标函数z1=2x+3y的最大值为a,目标函数z2=3x-2y的最小值为b,则a+b=( )
| A.10 | B.-2 | C.8 | D.6 |
在平面直角坐标系xoy中,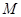 为不等式组
为不等式组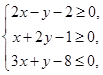 所表示的区域上一动点,则直线
所表示的区域上一动点,则直线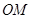 斜率的最小值为( )
斜率的最小值为( )
| A.2 | B.1 | C.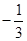 | D.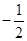 |
已知变量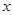 ,
,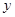 满足约束条件
满足约束条件 ,则
,则 的最小值为( )
的最小值为( )
| A.3 | B.1 | C.-5 | D.-6 |
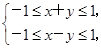 则点(x,y)在圆面x2+y2≤
则点(x,y)在圆面x2+y2≤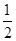 内部的概率为( )
内部的概率为( )