题目内容
设变量x,y满足约束条件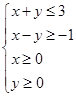 且目标函数z1=2x+3y的最大值为a,目标函数z2=3x-2y的最小值为b,则a+b=( )
且目标函数z1=2x+3y的最大值为a,目标函数z2=3x-2y的最小值为b,则a+b=( )
| A.10 | B.-2 | C.8 | D.6 |
D
解析试题分析:先作出约束条件的可行域图形,分将目标函数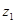 、
、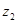 转变为函数
转变为函数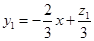 、
、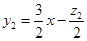 ,在坐标系中分别作出对应函数
,在坐标系中分别作出对应函数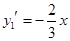 、
、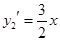 图像,考虑到函数
图像,考虑到函数 中
中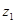 的系数符号为正,所以将函数
的系数符号为正,所以将函数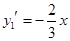 的图像在可行域范围内向上平移,直到可行域的最上顶点A,并求出该顶点坐标,代入目标函数即可求出
的图像在可行域范围内向上平移,直到可行域的最上顶点A,并求出该顶点坐标,代入目标函数即可求出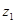 的最大值
的最大值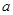 ;同理,考虑到函数
;同理,考虑到函数 中
中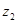 的系数符号为负,所以将函数
的系数符号为负,所以将函数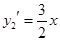 的图像在可行域范围内向上平移,直到可行域的最上顶点B,并求出该顶点坐标,代入目标函数即可求出
的图像在可行域范围内向上平移,直到可行域的最上顶点B,并求出该顶点坐标,代入目标函数即可求出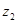 的最小值
的最小值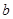 .最后可求出
.最后可求出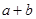 的值(如下图所示).
的值(如下图所示).
考点:线性规划

练习册系列答案
相关题目
设变量x,y满足约束条件 ,则
,则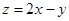 的取值范围是( )
的取值范围是( )
A. | B. |
C.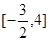 | D. |
若变量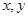 满足约束条件
满足约束条件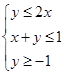 ,则
,则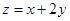 的最大值为 ( )
的最大值为 ( )
A.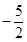 | B.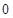 | C.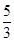 | D.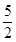 |
设变量x、y满足 则目标函数z=2x+y的最小值为( )
则目标函数z=2x+y的最小值为( )
| A.6 | B.4 | C.2 | D.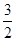 |
已知 、
、 满足约束条件
满足约束条件 ,则
,则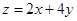 的最小值是( )
的最小值是( )
A. | B. | C. | D. |
设变量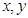 满足约束条件
满足约束条件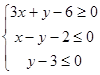 ,且目标函数
,且目标函数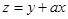 的最小值为-7,则
的最小值为-7,则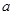 的值为( )
的值为( )
| A.-2 | B.-4 | C.-1 | D.1 |
设 的两个极值点分别是
的两个极值点分别是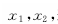 若
若
 (-1,0),则2a+b的取值范围是( )
(-1,0),则2a+b的取值范围是( )
| A.(1,7) | B.(2,7) | C.(1,5) | D.(2,5) |
已知实数x,y满足 则目标函数z=x-y的最小值为( ).
则目标函数z=x-y的最小值为( ).
| A.-2 | B.5 | C.6 | D.7 |
 和
和 内分别取一个数,记为
内分别取一个数,记为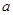 和
和 ,则方程
,则方程 表示离心率小于
表示离心率小于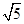 的双曲线的概率为( )
的双曲线的概率为( )