题目内容
函数f(x)满足:(ⅰ)?x∈R,f(x+2)=f(x),(ⅱ)x∈[-1,1],f(x)=-x2+1.给出如下三个结论:①函数f(x)在区间[1,2]单调递减;
②函数f(x)在点
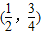 处的切线方程为4x+4y-5=0;
处的切线方程为4x+4y-5=0;③若[f(x)]2-2f(x)+a=0有实根,则a的取值范围是0≤a≤1.
其中正确结论的个数是( )
A.0
B.1
C.2
D.3
【答案】分析:利用函数的周期性与单调性判断①的正误;利用函数的切线方程判断②的正误;通过函数的值域判断③的正误.
解答:解:因为函数f(x)满足:(i)?x∈R,f(x+2)=f(x),( ii)x∈[-1,1],f(x)=-x2+1.
对于①,由题意可知函数在[-1,0]上是增函数,函数的周期为2,所以函数f(x)在区间[1,2]单调递减,是不正确的;
对于②,函数x∈[-1,1],f(x)=-x2+1,所以f′(x)=-2x,在点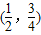 处的切线的斜率为:-1,
处的切线的斜率为:-1,
切线方程为:y- =-(x-
=-(x- )即切线方程为4x+4y-5=0,正确;
)即切线方程为4x+4y-5=0,正确;
对于③,函数f(x)∈[0,1],若[f(x)]2-2f(x)+a=0有实根,
所以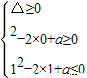 ,
,
可得0≤a≤1,则a的取值范围是0≤a≤1.正确.
故选C.
点评:本题考查命题的真假,函数的导数的应用切线方程的求法,二次函数根的分布,数列求和,以及函数的零点,考查知识面广,解答需要仔细认真.
解答:解:因为函数f(x)满足:(i)?x∈R,f(x+2)=f(x),( ii)x∈[-1,1],f(x)=-x2+1.
对于①,由题意可知函数在[-1,0]上是增函数,函数的周期为2,所以函数f(x)在区间[1,2]单调递减,是不正确的;
对于②,函数x∈[-1,1],f(x)=-x2+1,所以f′(x)=-2x,在点
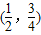 处的切线的斜率为:-1,
处的切线的斜率为:-1,切线方程为:y-
 =-(x-
=-(x- )即切线方程为4x+4y-5=0,正确;
)即切线方程为4x+4y-5=0,正确;对于③,函数f(x)∈[0,1],若[f(x)]2-2f(x)+a=0有实根,
所以
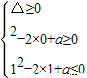 ,
,可得0≤a≤1,则a的取值范围是0≤a≤1.正确.
故选C.
点评:本题考查命题的真假,函数的导数的应用切线方程的求法,二次函数根的分布,数列求和,以及函数的零点,考查知识面广,解答需要仔细认真.

练习册系列答案
相关题目