题目内容
设P（x，y），其中x，y∈N，则满足x+y≤4的点P的个数为
15
15
．分析：欲求满足x+y≤4的点的个数，先在直角坐标系中画出满足x+y≤4的平面区域，后在区域中一一找出整数点即可．
解答：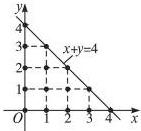
解：如图所示，
用数形结合法知共有15个满足x+y≤4的点P．
分别为（0，0），（0，1），（0，2），（0，3），（0，4），（1，0），（1，1），（1，2），（1，3），（2，0），（2，1），（2，2），（3，0），（3，1），（4，0）
故答案为：15．
解：如图所示，用数形结合法知共有15个满足x+y≤4的点P．
分别为（0，0），（0，1），（0，2），（0，3），（0，4），（1，0），（1，1），（1，2），（1，3），（2，0），（2，1），（2，2），（3，0），（3，1），（4，0）
故答案为：15．
点评：借助于平面区域特性，用几何方法处理代数问题，体现了数形结合思想、化归思想．属于基础题．
练习册系列答案
相关题目