题目内容
在△ABC中,角A,B,C的对边长分别为a,b,c,若c-a等于AC边上的高h,则sin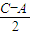 +cos
+cos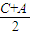 的值是( )
的值是( )A.1
B.

C.

D.-1
【答案】分析:由AC边上的高为c-a,由AC=b,表示出三角形的面积,再由a,c及sinB,利用三角形的面积公式表示出面积,两者相等列出关系式,利用正弦定理化简后,根据sinB不为0,得到sinA-sinC=sinAsinC,左边利用和差化积公式变形,右边利用积化和差公式变形,表示出2cos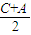 sin
sin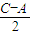 ,将所求式子平方并利用完全平方公式展开,第一、三项利用二倍角的余弦函数公式化简,将表示出的2cos
,将所求式子平方并利用完全平方公式展开,第一、三项利用二倍角的余弦函数公式化简,将表示出的2cos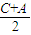 sin
sin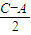 代入,求出值,再由c-a大于0,得到C大于A,可得出
代入,求出值,再由c-a大于0,得到C大于A,可得出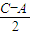 的范围,进而确定出sin
的范围,进而确定出sin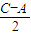 大于0,由三角形内角和定理得到
大于0,由三角形内角和定理得到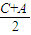 =90°-
=90°-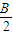 ,得出
,得出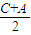 的范围,进而确定出cos
的范围,进而确定出cos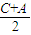 大于0,可得出所求式子大于0,开方即可求出值.
大于0,可得出所求式子大于0,开方即可求出值.
解答:解:∵S△ABC= acsinB=
acsinB= b(a-c),
b(a-c),
∴acsinB=b(a-c),
利用正弦定理化简得:sinAsinBsinC=sinB(sinA-sinC),
∵sinB≠0,
∴sinA-sinC=sinAsinC,
∴2cos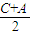 sin
sin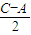 =
= [cos(A-C)-cos(A+C)],
[cos(A-C)-cos(A+C)],
又cos(A-C)=1-2sin2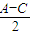 ,cos(A+C)=2cos2
,cos(A+C)=2cos2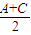 -1,
-1,
∴(sin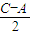 +cos
+cos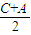 )2=sin2
)2=sin2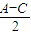 +2sin
+2sin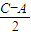 +cos
+cos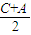 +cos2
+cos2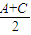
= [1-cos(C-A)]+
[1-cos(C-A)]+ [cos(C-A)-cos(A+C)]+
[cos(C-A)-cos(A+C)]+ [1+cos(C+A)]=1,
[1+cos(C+A)]=1,
∵c-a>0,∴C>A,
∴0<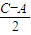 <90°,
<90°,
∴sin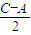 >0,
>0,
又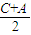 =90°-
=90°- ,且0<90°-
,且0<90°-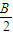 <90°,
<90°,
∴cos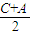 >0,
>0,
∴sin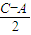 +cos
+cos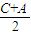 >0,
>0,
则sin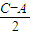 +cos
+cos =1.
=1.
故选A
点评:此题考查了三角形的和差化积公式,二倍角的余弦函数公式,正弦定理,三角形的面积公式,以及完全平方公式的运用,熟练掌握定理及公式是解本题的关键.
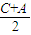 sin
sin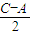 ,将所求式子平方并利用完全平方公式展开,第一、三项利用二倍角的余弦函数公式化简,将表示出的2cos
,将所求式子平方并利用完全平方公式展开,第一、三项利用二倍角的余弦函数公式化简,将表示出的2cos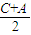 sin
sin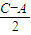 代入,求出值,再由c-a大于0,得到C大于A,可得出
代入,求出值,再由c-a大于0,得到C大于A,可得出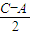 的范围,进而确定出sin
的范围,进而确定出sin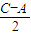 大于0,由三角形内角和定理得到
大于0,由三角形内角和定理得到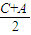 =90°-
=90°-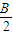 ,得出
,得出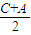 的范围,进而确定出cos
的范围,进而确定出cos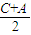 大于0,可得出所求式子大于0,开方即可求出值.
大于0,可得出所求式子大于0,开方即可求出值.解答:解:∵S△ABC=
 acsinB=
acsinB= b(a-c),
b(a-c),∴acsinB=b(a-c),
利用正弦定理化简得:sinAsinBsinC=sinB(sinA-sinC),
∵sinB≠0,
∴sinA-sinC=sinAsinC,
∴2cos
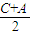 sin
sin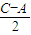 =
= [cos(A-C)-cos(A+C)],
[cos(A-C)-cos(A+C)],又cos(A-C)=1-2sin2
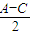 ,cos(A+C)=2cos2
,cos(A+C)=2cos2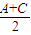 -1,
-1,∴(sin
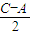 +cos
+cos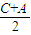 )2=sin2
)2=sin2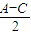 +2sin
+2sin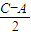 +cos
+cos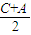 +cos2
+cos2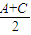
=
 [1-cos(C-A)]+
[1-cos(C-A)]+ [cos(C-A)-cos(A+C)]+
[cos(C-A)-cos(A+C)]+ [1+cos(C+A)]=1,
[1+cos(C+A)]=1,∵c-a>0,∴C>A,
∴0<
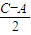 <90°,
<90°,∴sin
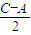 >0,
>0,又
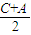 =90°-
=90°- ,且0<90°-
,且0<90°-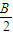 <90°,
<90°,∴cos
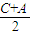 >0,
>0,∴sin
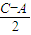 +cos
+cos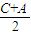 >0,
>0,则sin
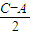 +cos
+cos =1.
=1.故选A
点评:此题考查了三角形的和差化积公式,二倍角的余弦函数公式,正弦定理,三角形的面积公式,以及完全平方公式的运用,熟练掌握定理及公式是解本题的关键.

练习册系列答案
相关题目
在△ABC中,角A、B、C所对的边分别为a,b,c,若b2+c2-a2=
bc,且b=
a,则下列关系一定不成立的是( )
| 3 |
| 3 |
| A、a=c |
| B、b=c |
| C、2a=c |
| D、a2+b2=c2 |