题目内容
已知椭圆C:
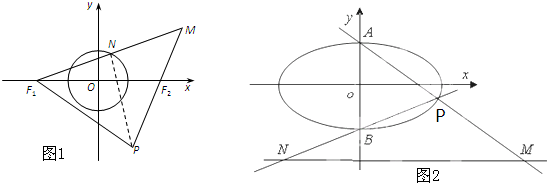
+y2=1的左右焦点分别为F1,F2,过F的值线l交椭圆C于A、B两点,过F2且平行于l的直线l1交椭圆C与M、N两点.
(1)求△ABF2的周长;
(2)求△ABM面积的最大值.
| x2 | 4 |
(1)求△ABF2的周长;
(2)求△ABM面积的最大值.
分析:(1)由椭圆的定义可得△ABF2的周长;
(2)设直线l的倾斜角为θ,当θ≠
时,求出点M到直线l的距离即为两条平行线间的距离,|AB|,计算三角形的面积,利用基本不等式求最值;当θ=
时,|AB|=1,d=2
,此时S△ABM=
<2,由此可得△ABM面积的最大值.
(2)设直线l的倾斜角为θ,当θ≠
| π |
| 2 |
| π |
| 2 |
| 3 |
| 3 |
解答:解:(1)由椭圆的定义可得△ABF2的周长=|AB|+AF2|+|BF2|=4a=8;
(2)设直线l的倾斜角为θ,当θ≠
时,l:y=tanθ(x+
),l1:y=tanθ(x-
)
点M到直线l的距离即为两条平行线间的距离:d=2
sinθ
∵|AB|=
=
∴S△ABM=
×
×2
sinθ=
≤
=2
当且仅当sinθ=
时,取等号
当θ=
时,|AB|=1,d=2
,此时S△ABM=
<2
∴△ABM面积的最大值为2.
(2)设直线l的倾斜角为θ,当θ≠
| π |
| 2 |
| 3 |
| 3 |
点M到直线l的距离即为两条平行线间的距离:d=2
| 3 |
∵|AB|=
2×
| ||
| 1-e2cos2θ |
| 1 | ||
1-
|
∴S△ABM=
| 1 |
| 2 |
| 1 | ||
1-
|
| 3 |
4
| ||
|
4
| ||
2
|
当且仅当sinθ=
| ||
| 3 |
当θ=
| π |
| 2 |
| 3 |
| 3 |
∴△ABM面积的最大值为2.
点评:本题考查椭圆的定义,考查三角形面积的计算,考查基本不等式的运用,属于中档题.

练习册系列答案
相关题目
 圆锥曲线上任意两点连成的线段称为弦.若圆锥曲线上的一条弦垂直于其对称轴,我们将该弦称之为曲线的垂轴弦.已知椭圆C:
圆锥曲线上任意两点连成的线段称为弦.若圆锥曲线上的一条弦垂直于其对称轴,我们将该弦称之为曲线的垂轴弦.已知椭圆C: