题目内容
(本小题满分12分)(注意:在试题卷上作答无效)
已知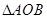 的顶点A在射线
的顶点A在射线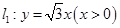 上,
上, 、
、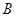 两点关于x轴对称,0为坐标原点,
两点关于x轴对称,0为坐标原点,
且线段AB上有一点M满足 当点A在
当点A在 上移动时,记点M的轨迹为W.
上移动时,记点M的轨迹为W.
(Ⅰ)求轨迹W的方程;
(Ⅱ)设 是否存在过
是否存在过 的直线
的直线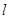 与W相交于P,Q两点,使得
与W相交于P,Q两点,使得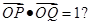 若存在,
若存在,
求出直线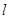 ;若不存在,说明理由.
;若不存在,说明理由.
【答案】
解:(Ⅰ)因为A,B两点关于x轴对称,
所以AB边所在直线与y轴平行.
设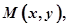 由题意,得
由题意,得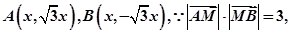

所以点M的轨迹W的方程为 …………4分
…………4分
(Ⅱ)假设存在,设
当直线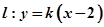 时,由题意,知点P,Q的坐标是方程组
时,由题意,知点P,Q的坐标是方程组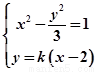 的解,
的解,
消去y得  …………6分
…………6分
所以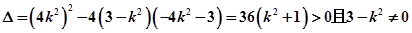
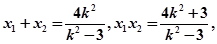 …………7分
…………7分
 直线
直线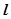 与双曲线的右支(即W)相交两点P,Q,
与双曲线的右支(即W)相交两点P,Q,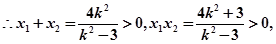
即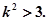 ①…………8分
①…………8分
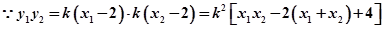

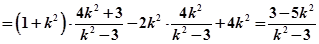 …………10分
…………10分
要使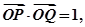 则必须有
则必须有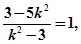 解得
解得 代入①不符合。
代入①不符合。
所以不存在直线 ,使得
,使得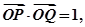 …………11分
…………11分
当直线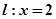 时,
时,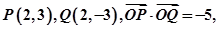 不符合题意,
不符合题意,
综上:不存在直线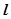 ,使得
,使得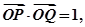 …………12分
…………12分
【解析】略

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目