题目内容
已知f(x)=log2(x-2),若实数m,n满足f(m)+f(2n)=3,则m+n的最小值为( )
| A.5 | B.7 | C.8 | D.9 |
B
由已知得log2(m-2)+log2(2n-2)=3,即log2[(m-2)(2n-2)]=3,
因此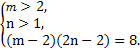 于是n=
于是n=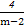 +1.
+1.
所以m+n=m+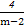 +1=m-2+
+1=m-2+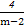 +3≥2
+3≥2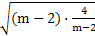 +3=7.当且仅当m-2=
+3=7.当且仅当m-2=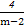 ,即m=4时等号成立,此时m+n取最小值7.
,即m=4时等号成立,此时m+n取最小值7.
因此
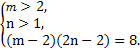 于是n=
于是n=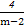 +1.
+1.所以m+n=m+
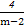 +1=m-2+
+1=m-2+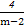 +3≥2
+3≥2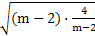 +3=7.当且仅当m-2=
+3=7.当且仅当m-2=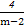 ,即m=4时等号成立,此时m+n取最小值7.
,即m=4时等号成立,此时m+n取最小值7.
练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
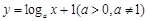 的图象恒过定点A,若点A在直线
的图象恒过定点A,若点A在直线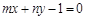 上,其中
上,其中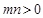 ,则
,则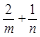 的最小值为_______.
的最小值为_______.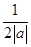 +
+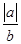 的最小值为 .
的最小值为 .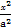 -
-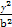 =1与
=1与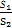 的最大值为 .
的最大值为 . 的最小值是( )
的最小值是( )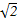
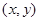 满足约束条件
满足约束条件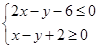 ,若目标函数
,若目标函数
 的最大值为40,则
的最大值为40,则 的最小值为( )
的最小值为( )
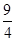
 (x+1)图象上异于原点的动点,且该图象在点P处的切线的倾斜角为θ,则θ的取值范围是________.
(x+1)图象上异于原点的动点,且该图象在点P处的切线的倾斜角为θ,则θ的取值范围是________.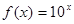 ,对于实数
,对于实数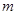 、
、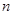 、
、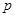 有
有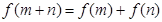 ,
,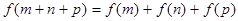 ,则
,则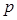 的最大值等于 .
的最大值等于 . +
+ ,q=
,q= ·
· (m、n、a、b、c、d均为正数),
(m、n、a、b、c、d均为正数),