题目内容
已知函数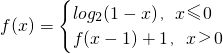
，则f（2011）=
- A.2012
- B.2011
- C.2010
- D.2009
B
分析：考虑到f（2011 ）中自变量的值x=2011，若逐步递推，计算量较大．再结合第二段解析式，寻找规律：当x＞0时，f（x）-f（x-1）=1，数列{f（n）}（n是自然数）是以1为公差，以f（0）为首项的等差数列，问题容易获解．
解答：由已知，当x＞0时，f（x）-f（x-1）=1，
所以数列{f（n）}（n是自然数）是以1为公差，以f（0）为首项的等差数列
因为f（0）=log2（1-0）=log21=0，
所以根据等差数列的通项公式得出f（2011）=f（0）+2011×1=0+2011=2011
故选B．
点评：本题考查分段函数求函数值，等差数列的判定及通项公式．确定出数列{f（n）}（n是自然数）是等差数列，是减少递推运算量的关键．
分析：考虑到f（2011 ）中自变量的值x=2011，若逐步递推，计算量较大．再结合第二段解析式，寻找规律：当x＞0时，f（x）-f（x-1）=1，数列{f（n）}（n是自然数）是以1为公差，以f（0）为首项的等差数列，问题容易获解．
解答：由已知，当x＞0时，f（x）-f（x-1）=1，
所以数列{f（n）}（n是自然数）是以1为公差，以f（0）为首项的等差数列
因为f（0）=log2（1-0）=log21=0，
所以根据等差数列的通项公式得出f（2011）=f（0）+2011×1=0+2011=2011
故选B．
点评：本题考查分段函数求函数值，等差数列的判定及通项公式．确定出数列{f（n）}（n是自然数）是等差数列，是减少递推运算量的关键．
练习册系列答案
相关题目