题目内容
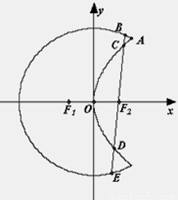
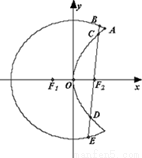
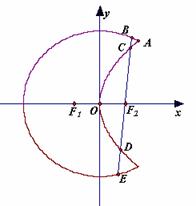
如图,曲线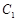 是以原点O为中心、
是以原点O为中心、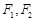 为焦点的椭圆的一部分,曲线
为焦点的椭圆的一部分,曲线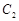 是以O为顶点、
是以O为顶点、 为焦点的抛物线的一部分,A是曲线
为焦点的抛物线的一部分,A是曲线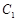 和
和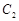 的交点
的交点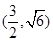 且
且
 为钝角.
为钝角.
(1)求曲线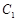 和
和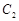 的方程;
的方程;
(2)过 作一条与
作一条与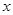 轴不垂直的直线,分别与曲线
轴不垂直的直线,分别与曲线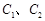 依次交于B、C、D、E四点,若G为CD中点、H为BE中点,问
依次交于B、C、D、E四点,若G为CD中点、H为BE中点,问 是否为定值?若是求出定值;若不是说明理由.
是否为定值?若是求出定值;若不是说明理由.
【答案】
(1)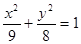 ,
,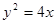 (2)3
(2)3
【解析】本题考查椭圆、抛物线的标准方程,考查直线与椭圆、抛物线的位置关系,考查韦达定理的运用,考查学生的计算能力,联立方程,正确运用韦达定理是关键
(Ⅰ)设曲线C2所在的抛物线的方程为y2=2px,将A( 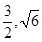 )
)
)代入可得p的值,利用椭圆的定义,可得曲线C1所在的椭圆的方程;
(Ⅱ)设B(x1,y1),E(x2,y2),C(x3,y3),D(x4,y4),过F2与x轴不垂直的直线为x=ty+1,与椭圆方程联立,利用韦达定理可得|y1 -y2|,同理可知|y3-y4| 。
解:(本小题满分12分)(Ⅰ)
椭圆方程为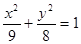 ,抛物线方程为
,抛物线方程为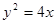 。 ……………5分
。 ……………5分

则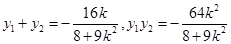
同理,将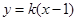 代入
代入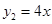 得:
得: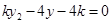
则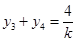 ,
,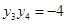 …………8分
…………8分
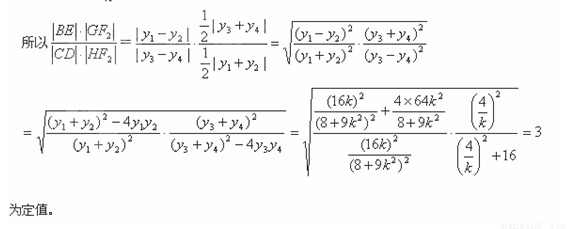 …………12分
…………12分

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
 是以原点O为中心、
是以原点O为中心、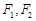 为焦点的椭圆的一部分,曲线
为焦点的椭圆的一部分,曲线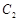 是以O为顶点、
是以O为顶点、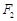 为焦点的抛物线的一部分,A是曲线
为焦点的抛物线的一部分,A是曲线 为钝角,若
为钝角,若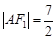 ,
,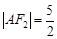 .
. 轴不垂直的直线,分别与曲线
轴不垂直的直线,分别与曲线 依次交于B、C、D、E四点,若G为CD中点、H为BE中点,问
依次交于B、C、D、E四点,若G为CD中点、H为BE中点,问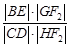 是否为定值?若是求出定值;若不是说明理由.
是否为定值?若是求出定值;若不是说明理由. 是以原点O为中心、
是以原点O为中心、 为焦点的椭圆的一部分,曲线
为焦点的椭圆的一部分,曲线 是以O为顶点、
是以O为顶点、 为焦点的抛物线的一部分,A是曲线
为焦点的抛物线的一部分,A是曲线 为钝角,若
为钝角,若 ,
, .
. 轴不垂直的直线,分别与曲线
轴不垂直的直线,分别与曲线 依次交于B、C、D、E四点,若G为CD中点、H为BE中点,问
依次交于B、C、D、E四点,若G为CD中点、H为BE中点,问 是否为定值?若是求出定值;若不是说明理由.
是否为定值?若是求出定值;若不是说明理由.
 是以原点O为中心、
是以原点O为中心、 为焦点的椭圆的一部分,曲线
为焦点的椭圆的一部分,曲线 是以O为顶点、
是以O为顶点、 为焦点的抛物线的一部分,A是曲线
为焦点的抛物线的一部分,A是曲线 为钝角,若
为钝角,若 ,
,
 轴不垂直的直线,分别与曲线
轴不垂直的直线,分别与曲线 依次交于B、C、D、E四点,若G为CD中点、H为BE中点,问
依次交于B、C、D、E四点,若G为CD中点、H为BE中点,问 是否为定值?若是求出定值;若不是说明理由
是否为定值?若是求出定值;若不是说明理由