Question

（本小题满分12分）

如图，直二面角D—AB—E中，四边形ABCD是边长为2的正方形，AE=EB，F为CE上的点，且BF⊥平面ACE.

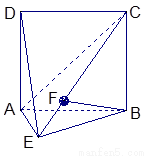
（Ⅰ）求证AE⊥平面BCE；

（Ⅱ）求二面角B—AC—E的大小；

 

Answer 1

【答案】

（I）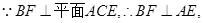

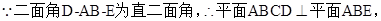
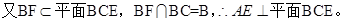
（II）连结AC、BD交于G，连结FG，

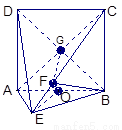
∵ABCD为正方形，∴BD⊥AC，∵BF⊥平面ACE，∴FG⊥AC，∠FGB为二面角B-AC-E的平面角，由（I）可知，AE⊥平面BCE，∴AE⊥EB，又AE=EB，AB=2，AE=BE=，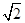

在直角三角形BCE中，CE=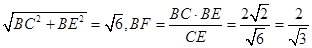

 

在正方形中，BG=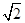，在直角三角形BFG中，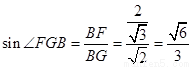

 

∴二面角B-AC-E为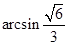

（III）由（II）可知，在正方形ABCD中，BG=DG，D到平面ACB的距离等于B到平面ACE的距离，BF⊥平面ACE，线段BF的长度就是点B到平面ACE的距离，即为D到平面ACE的距离所以D到平面的距离为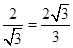

 

另法：过点E作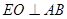交AB于点O. OE=1.

∵二面角D—AB—E为直二面角，∴EO⊥平面ABCD.

设D到平面ACE的距离为h，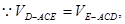 

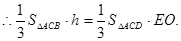
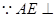平面BCE，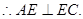 

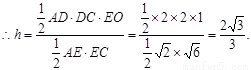
∴点D到平面ACE的距离为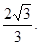

解法二：

（Ⅰ）同解法一.

（Ⅱ）以线段AB的中点为原点O，OE所在直线为x轴，AB所在直线为y轴，过O点平行于AD的直线为z轴，建立空间直角坐标系O—xyz，如图.

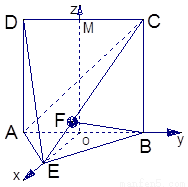
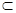面BCE，BE面BCE， ，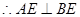

在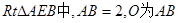的中点，

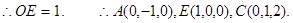
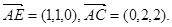 设平面AEC的一个法向量为，

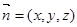则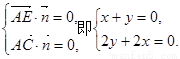

 

解得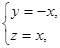

    

令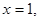得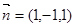是平面AEC的一个法向量.

又平面BAC的一个法向量为，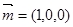

 

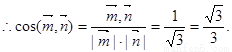
∴二面角B—AC—E的大小为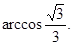

 

（III）∵AD//z轴，AD=2，∴，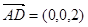

∴点D到平面ACE的距离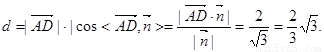

 

【解析】略