题目内容
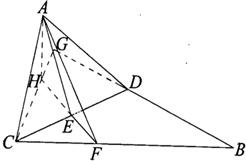
 如图,在Rt△ABC中,∠ACB=90°,∠B=30°,D,E分)别为AB,CD的中点,AE的延长线交CB于F.现将△ACD沿CD折起,折成二面角A-CD-B,连接AF.
如图,在Rt△ABC中,∠ACB=90°,∠B=30°,D,E分)别为AB,CD的中点,AE的延长线交CB于F.现将△ACD沿CD折起,折成二面角A-CD-B,连接AF.
(I)求证:平面AEF⊥平面CBD;
(II)当AC⊥BD时,求二面角A-CD-B大小的余弦值.
 解:
解:
(I)证明:在Rt△ABC中,D为AB的中点,得AD=CD=DB,
又∠B=30°,得△ACD是正三角形,
又E是CD的中点,得AF⊥CD.
折起后,AE⊥CD,EF⊥CD,
又AE∩EF=E,AE?平面AED,EF?平面AEF,
故CD⊥平面AEF,
又CD?平面CDB,
故平面AEF⊥平面CBD.
(II)过点A作AH⊥EF,垂足H落在FE的延长线,
因为CD⊥平面AEF,所以CD⊥AH,
所以AH⊥平面CBD.
连接CH并延长交BD的延长线于G,
由已知AC⊥BD,得CH⊥BD,可得BD垂直于面AHC,从而得到BD垂直于线CG
可得∠CGB=90°,
因此△CEH∽△CGD,
则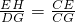 ,
,
设AC=a,易得
∠GDC=60°,DG= ,
,
代入上式得EH=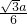 ,
,
又EA=
故cos∠HEA= .
.
又∵AE⊥CD,EF⊥CD,
∴∠AEF即为所求二面角的平面角,
故二面角A-CD-B大小的余弦值为- .
.
分析:(I)欲证平面AEF⊥平面CBD,根据面面垂直的判定定理可知在平面CDB内一直线与平面AEF垂直,根据翻折前后有些垂直关系不变AE⊥CD,EF⊥CD,又AE∩EF=E,AE?平面AED,EF?平面AEF,满足线面垂直的判定定理,则CD⊥平面AEF,又CD?平面CDB,满足定理所需条件;
(II)先作出二面角的平面角,过点A作AH⊥EF,垂足H落在FE的延长线,连接CH并延长交BD的延长线于G,根据二面角平面角的定义可知∠AEF即为所求二面角的平面角,在三角形AEF中求出此角即可求出所求.
点评:本题主要考查了面面垂直的判定,以及二面角平面角的度量,考查学生空间想象能力,逻辑思维能力,是中档题.

练习册系列答案
相关题目
 如图,在Rt△ABC中,∠C=90°,D为BC上一点,∠DAC=30°,BD=2,AB=2
如图,在Rt△ABC中,∠C=90°,D为BC上一点,∠DAC=30°,BD=2,AB=2| 3 |
A、2
| ||||
| B、3 | ||||
C、
| ||||
D、
|
 如图,在Rt△ABC中,AC=1,BC=x,D是斜边AB的中点,将△BCD沿直线CD翻折,若在翻折过程中存在某个位置,使得CB⊥AD,则x的取值范围是( )
如图,在Rt△ABC中,AC=1,BC=x,D是斜边AB的中点,将△BCD沿直线CD翻折,若在翻折过程中存在某个位置,使得CB⊥AD,则x的取值范围是( )A、(0,
| ||||
B、(
| ||||
C、(
| ||||
| D、(2,4] |
 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E.
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E. 如图,在Rt△ABC中,∠ABC=90°,BA=BC=2,AE⊥平面ABC,CD⊥平面ABC,CE交AD于点P.
如图,在Rt△ABC中,∠ABC=90°,BA=BC=2,AE⊥平面ABC,CD⊥平面ABC,CE交AD于点P. 8.如图,在Rt△ABC中,∠CAB=90°,AB=2,AC=
8.如图,在Rt△ABC中,∠CAB=90°,AB=2,AC=