题目内容
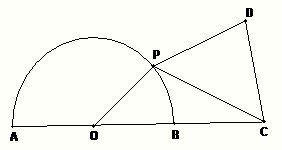 如图:已知圆O的直径是2,点C在直径AB的延长线上,BC=1,点P是圆O上的一个动点,以PC为边作正三角形PCD,且点D与圆心分别在PC的两侧,求四边形OPDC面积的最大值.
如图:已知圆O的直径是2,点C在直径AB的延长线上,BC=1,点P是圆O上的一个动点,以PC为边作正三角形PCD,且点D与圆心分别在PC的两侧,求四边形OPDC面积的最大值.
分析:设∠POB=θ,将面积表示为角的函数,再利用三角函数求最值的方法求最值.
解答:解:设∠POB=θ.在△POC中,由余弦定理得:PC2=OP2+OC2-2OP•OC•cosθ=5-4cosθ
所以S=S△OPC+S△PCD=2sin(θ-
)+
,当θ-
=
时,即θ=
π时,
四边形OPDC面积的最大值为 2+
.
所以S=S△OPC+S△PCD=2sin(θ-
| π |
| 3 |
| 5 |
| 4 |
| 3 |
| π |
| 3 |
| π |
| 2 |
| 5 |
| 6 |
四边形OPDC面积的最大值为 2+
| 5 |
| 4 |
| 3 |
点评:本题通过引进角,利用余弦定理求边长,从而构建函数,再求函数的最值.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
 如图,已知圆O的直径AB=4,定直线L到圆心的距离为4,且直线L垂直直线AB.点P是圆O上异于A、B的任意一点,直线PA、PB分别交L与M、N点.
如图,已知圆O的直径AB=4,定直线L到圆心的距离为4,且直线L垂直直线AB.点P是圆O上异于A、B的任意一点,直线PA、PB分别交L与M、N点. 如图,已知圆O的直径AB长度为4,点D为线段AB上一点,且
如图,已知圆O的直径AB长度为4,点D为线段AB上一点,且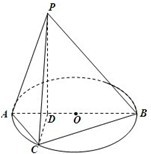 (2013•佛山一模)如图,已知圆O的直径AB长度为4,点D为线段AB上一点,且
(2013•佛山一模)如图,已知圆O的直径AB长度为4,点D为线段AB上一点,且