题目内容
已知函数 (
(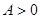 ,
,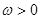 ,
,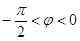 )的图像与
)的图像与 轴的交点
轴的交点
为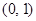 ,它在
,它在 轴右侧的第一个最高点和第一个最低点的坐标分别为
轴右侧的第一个最高点和第一个最低点的坐标分别为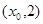 和
和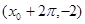
(1)求函数 的解析式;
的解析式;
(2)若锐角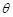 满足
满足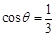 ,求
,求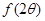 的值.
的值.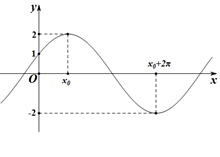
(1) ;(2)
;(2)  .
.
解析试题分析:(1)根据函数的图象,逐一确定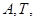 然后代入点(0,1)求解
然后代入点(0,1)求解 ,进而确定函数的解析式;(2)借助第一问的函数解析式,确定
,进而确定函数的解析式;(2)借助第一问的函数解析式,确定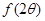 ,然后借助两角和的余弦公式展开求解其值.
,然后借助两角和的余弦公式展开求解其值.
试题解析:(1)由题意可得 ,
, 即
即 ,
,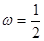 3分
3分 ,
,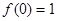 ,
,
由 且
且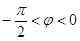 ,得
,得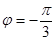 ,
,
函数 . 6分
. 6分
(2)由于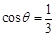 且
且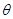 为锐角,所以
为锐角,所以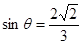 .
.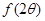
 10分
10分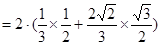
 12分
12分
考点:1.三角函数的图象;(2)函数的解析式;(3)三角函数求值.

练习册系列答案
相关题目
已知某海滨浴场的海浪高达y(米)是时间t(0≤t≤24,单位:小时)的函数,记作y=f(t).下表是某日各时的浪高数据.
| t(时) | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y(米) | 1.5 | 1.0 | 0.5 | 1.0 | 1.5 | 1.0 | 0.5 | 0.99 | 1.5 |
(1)根据以上数据,求出函数y=Acosωt+b的最小正周期T、振幅A及函数表达式;
(2)依据规定,当海浪高度高于1米时才对冲浪爱好者开放,请依据(1)的结论,判断一天内的上午8:00至晚上20:00之间,有多长时间可供冲浪者进行运动?
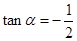 ,求
,求 的值;
的值;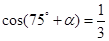 ,且
,且 ,求
,求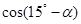 的值.
的值.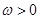 ,函数
,函数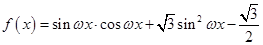 的最小正周期为
的最小正周期为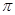 .
.
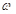 的值;
的值; 在区间
在区间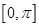 上的图象,并根据图象写出其在区间
上的图象,并根据图象写出其在区间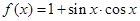 .(1)求函数
.(1)求函数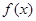 的最小正周期和最小值;(2)若
的最小正周期和最小值;(2)若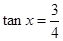 ,
,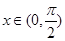 ,求
,求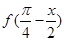 的值.
的值.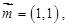 向量
向量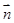 与向量
与向量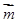 的夹角为
的夹角为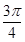 ,且
,且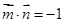 .
.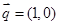 共线,向量
共线,向量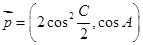 ,其中
,其中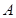 、
、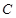 为
为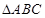 的内角,且
的内角,且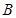 、
、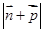 的取值范围.
的取值范围. ,
, 在
在 上的最大值与最小值;
上的最大值与最小值; 使得
使得 对任意
对任意 恒成立,求
恒成立,求 的值.
的值.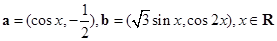 , 设函数
, 设函数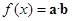 .
.  上的最大值和最小值.
上的最大值和最小值.  的图象过点(1,2),相邻两条对称轴间的距离为2,且
的图象过点(1,2),相邻两条对称轴间的距离为2,且 的最大值为2.
的最大值为2. ;
;  ;
; 在区间[1,4]上恰有一个零点,求
在区间[1,4]上恰有一个零点,求 的范围.
的范围.